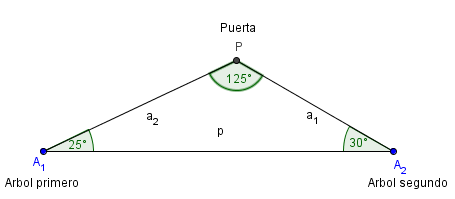
Calcule la distancia desde la puerta de la casa al segundo de los árboles y la distancia que separa a los dos árboles
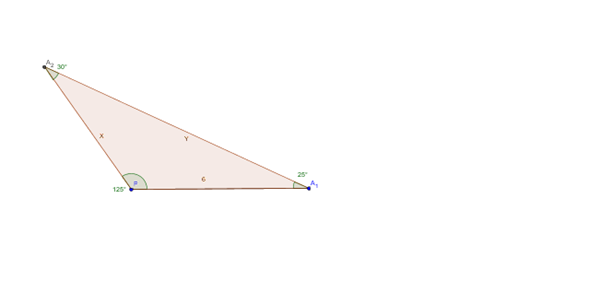
En el patio de una casa hay dos árboles. Uno de ellos está a una distancia de 6 metros de la puerta de la casa. Si nos alejamos en él, observamos que el ángulo que forman las líneas que unen éste árbol con la puerta de la casa y éste árbol con el otro es de 25 grados. Si vamos al segundo árbol, observamos que el ángulo que forman lad líneas que unen éste árbol con la puerta de la casa y con el otro árbol es de 30 grados. Calcule la distancia desde la puerta de la casa al segundo de los árboles y la distancia que separa a los dos árboles.
2 respuestas
Aplicando el Teorema del seno:
$$\begin{align}&\frac{6}{sen30º}=\frac{y}{sen125º}=\frac{x}{sen25º}\\&\\&y=\frac{6·sen125º}{sen30º}=9,8298 m\\&\\&x=\frac{6·sen25º}{sen30º}=5,0714 m\end{align}$$
·
Hagamos el gráfico para entenderlo:
He puesto ya el ángulo de 125º que es el que falta para completar los 180º del triángulo.
P= 180º-25º-30º = 125º
La distancia que nos dan es la del arból primero a la puerta, es la que tiene nombre a sub 2
Aplicando el teorema del seno.
$$\begin{align}&\frac{p}{sen\,P}=\frac{a_1}{sen\,A_1}=\frac {a_2}{sen\,A_2}\\&\\&\frac{p}{sen\, 125º}=\frac{a_1}{sen\,25º}=\frac{6}{sen\,30º}=12\\&\\&p=12·sen\,125º=9.82982m\\&\\&a_1=12·sen\,25º= 5.07142m\end{align}$$Y eso es todo.