Graficar las siguientes 2 funciones y determinar su dominio y rango: 1) y=1/x 2) y=x^2+4x+3/x+3

·

Debe mandarse un ejercicio en cada pregunta. Pero como el 1/x no tiene nada haré los dos.

1)

y=1/x

El dominio es Dom f = R-{0}

solo x=0 anula el denominador y hace que la operación esté indefinida.

El rango es el dominio de la inversa

x=1/y

f^(-1)(x) = 1/x

el dominio de la inversa es R-{0}

luego Rango f = R-{0}

·

2)

y=x^2+4x+3/x+3

nunca se puede escribir eso (normalmente), imagino que querías decir esto

y = (x^2+4x+3) / (x+3)

Siempre que haya un numerador o denominador compuesto de otras operaciones debe estar encerrado entre parénteisis, porque si no es imposible saber donde empiezan o terminan.

Y en contra de lo que piensa la gente de que se debe tomar tomar todo como numerador o todo como denominador la norma es la contraria, se toma el mínimo numerador y denominador, con lo cual lo que has escrito es:

$$\begin{align}&y = x^2+4x + \frac 3x+3\end{align}$$

Luego la función debe escribirse

y = (x^2+4x+3) / (x+3)

que estoy seguro es lo que querías decir

El dominio son todos los números reales salvo los que hacen 0 el denominador.

x+3=0

x=-3

Luego Dom f = R - {3}

Y el rango es el dominio de la función inversa. Es este un ejercicio complicado comparado con los otros que has mandado hasta el momento.

$$\begin{align}&y=\frac{x^2+4x+3}{x+3}\\&\\&y(x+3)=x^2+4x+3\\&\\&yx + 3y = x^2+4x+3\\&\\&x^2+(4x -yx) +(3-3y) =0\\&\\&x^2 +(4-y)x +(3-3y)=0\\&\\&\text{esto es una ecuación de segundo grado}\\&\\&x=\frac{-(4-y)\pm \sqrt{(4-y)^2 - 4(3-3y)}}{2}\\&\\&x=\frac{y-4\pm \sqrt{16-8y+y^2-12+12y}}{2}\\&\\&x=\frac{y-4\pm \sqrt{y^2+4y+4}}{2}\\&\\&x = \frac{y-4 \pm \sqrt{(y+2)^2}}{2}\\&\\&x=\frac{y-4\pm (y+2)}{2}=\\&\\&x_1=\frac{2y-2}{2}= y-1\\&\\&x_2=-3 \end{align}$$

Bueno, yo creo que esto que he hecho es muy complicado y no pienso que te hayan enseñado a hacerlo así. 

Vamos a reolver el rango de otra forma

Factorizamos el numerador

x^2 + 4x + 3 = (x+3)(x+1)

Entonces la función se puede simplificar si x es distinto de 3 y queda así.

f(x) = (x+3)(x+1) / (x+3)

f(x) =  x+1   si x distinta de 3

con lo cual el rango se calcula así:  dado un y veamos si existe x tal que f(x)=y

y = x+1

x=y-1

este x existe siempre que sea distinto de 3 luego no existe cuando

3 = y -1

y =4

Luego Rango f = R - {4}

Y las gráficas son:

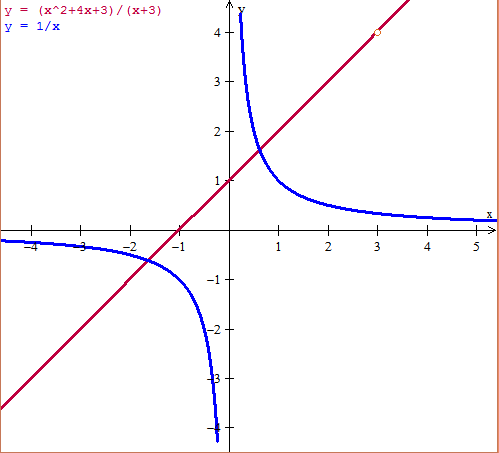
Y eso es todo.