Integrales de línea, como realizo parametrización dudas allí.

Diosa Lara!

·

La parametrización de un segmento de recta es la cosa más sencilla del mundo.

Recuerda como es la ecuación paramétrica de una recta. Dado un punto (xo, yo) y un vector (u, v) la ecuación paramétrica es

x(t) = xo + u·t

y(t) = yo + v·t

Fijate que para t=0 tendrás

x(0) = xo

y(0) = yo

y para t=1 tendrás

x(1) = xo + u

y(1)=yo + v

Entonces para un segmento entre (xo,yo) y (x1,y1)

si tomas el vector que los une (x1-xo, y1-yo) y parametrizas entre

0<=t<=1

tendrás

x(t) = xo + (x1-xo)t

y(t) = yo + (y1-yo)t

entonces para t=0

x(0) = xo 

y(0) = yo

x(1) = xo + (x1-xo)·1 = xo + x1 - xo = x1

y(1) = yo + (y1-yo)·1 = yo + y1 - yo = y1

Luego ahí tenemos la parametrización que nos lleva de un punto a otro a través de un segmento de recta.

Para el ejercicio la parametrización será

x(t) = 0 + (1-0)t  =  t

y(t) = 0 + (2-0)t  =  2t

con 0 <= t <= 1

Entonces la integral de línea por definición del campo escalar es:

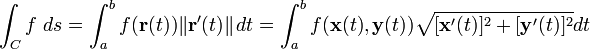
$$\begin{align}&\int_C \;\frac{ds}{x^2+y^2+4}=\\&\\&\int_0^1 \frac{\sqrt{1^2+2^2}}{t^2+4t^2+4}dt\end{align}$$

Y esa integral es facil aunque pueda costar un poquito resolverla, es un arcotangente, te dejo hacerla.

Y eso es todo.

Algo simple que quizás aun no lo veo:  Como es que mis limites llegan a ser 0<=t<=1 o en tal caso es dado por la parametrizacion dando valores a t mediante (0,0) y (1,2)???

La parametrización será entre el valor de t que al sustituirlo nos dé el punto (0,0) y el valor de t que al sustituirlo nos dé el punto (1,2). Por la forma de la parametrización se irán recorriendo los puntos intermedios para los valores de t comprendidos ente esos dos límites.

x(t) = t

y(t)= 2t

Para t=0 tenemos el punto

x(0)=0

y(0)=0

o sea, el punto (0,0)

Y para t=1 tenemos

x(1) = 1

x(2) = 2

Que es punto (1,2)

Luego la parameterización del segmento se consigue con los valores de t comprendidos entre 0 y 1

Perfecto ya logre comprender ese punto, una cosita antes de puntuar la pregunta, como es que x^2+y^2+4 paso a ser t^2+4t^2+4??

Porque tienes que sustituir x por la función parametrizada x(t) y y por la función y(t), es algo que forma parte de la teoría.

Como

x(t)=t

y(t)=2t

tendrás

x²+y²+4 = t²+(2t)²+4 = t²+4t²+4 = 5t²+4

Y eso es todo.