¿Como resolver las integrales impropias?
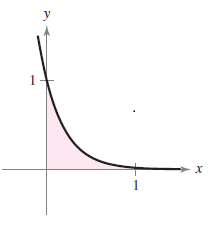
Explica por qué la integral es impropia y determina sí es divergente o convergente. En caso de ser convergente calcula el área.$$\begin{align}&∫_0^∞ e^(-x) dx\end{align}$$
$$\begin{align}&∫_0^21/(x-1)^2 dx\end{align}$$
1 respuesta
Respuesta de Valero Angel Serrano Mercadal
1
·
1)
Es impropia porque el límite superior es infinito.
Yo creo que sería mejor intentar calcularla primero para ver si es convergente o no es convergente. Porque si no se hace la integral habra que usar algún teorema de convergencia como que
e^x > x^2 para todo x>=0
0 < 1/e^x < 1/x^2
0 < e^(-x) < 1/x^2
Y como 1/x^2 converge por ser de la forma 1/x^n con n>1, entonces e^(-x) es convergente.
Pero cuando la integral se puede resolver lo más habitual es resolverla para saber si es convergente o no
$$\begin{align}&\int_0^{-\infty}e^{-x}dx=-e^{-x}\bigg|_0^{\infty}=\\&\\&-\lim_{x\to \infty}e^{-x}+e^0=0+1=1\end{align}$$-----
Y eso es todo, en lo posible debes mandar un ejercicio en cada pregunta.
