Ejercicio de física mecánica encuentre una tercera fuerza
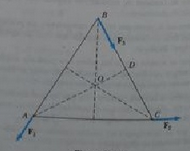
Dos fuerzas F1 y F2 actúan a lo largo de dos lados de un triangulo equilátero como se muestra en la figura, el punto 0 esta en la intersección de las altitudes del triangulo, encuentre una tercera fuerza F3 a aplicar en B y a lo largo de BC que haga cero el par de torsión total alrededor del punto 0 ¿qué pasa si? ¿Cambiara el par de torsión total si F3 se aplica no en B sino en cualquier otro punto a lo largo de BC?
1 respuesta
Lamentablemente no puedo abrir ninguno de los gráficos que estas enviando... ponelos de otra forma o explícame como los abro ...
Muchas gracias por tu ayuda mira aquí te muestro la gráfica...
Vamos por partes.
El triangulo equilatero tiene propiedades importantes. La alturas cortan a las bases por sus puntos medios... La alturas son siempre perpendiculares a las bases... El centro de masa del triangulo es la intersección de las tres alturas.
La alturas cortan al centro de masa ( Punto 0 ) en segmentos iguales desde cada base... Distancia centro de base - centro de masa (0) = 0.2828 a ( siendo lado triangulo = a).
El momento de las fuerzas F1 y F2 respecto de 0 será entonces...( yo estoy tomando como sentido + el del reloj y sentido - el contrario)...
M 1 (O)= - 0.2828a ( F1+F2)
Para equilibrarlo tendras que aplicar una F3 tal que 0.2828 a F3 = 0.2828a ( F1+F2) ...........o sea F3= F1 + F2. En cualquier punto a lo largo de la recta BC que apliques F3 tendrás el mismo resultado porque la distancia de la recta de accion del vector al centro de momentos O será siempre unica = 0.2828a
