Lo primero que debemos saber son las transformaciones que hay que aplicar en cada caso:
$$\begin{align}&Rectangular \to Polar\\&r=\sqrt{x^2+y^2}\\&\theta=arctg(\frac{y}{x})\\&\\&Polar \to Rectangular\\&x= r\ \cos \theta\\&y = r\ sen \theta\\&\\&\text{Veamos ahora cada caso}\\&a) x^2+y^2=a^2\\&Polar:\\&(r \cos \theta)^2+(r sen \theta)^2=a^2\\&r^2 \cos^2 \theta+ r^2 sen^2 \theta=a^2\\&r^2 (\cos^2 \theta+sen^2 \theta)=a^2\\&r^2=a^2\\&r=|a|\\&\\&b) y=4\\&r sen \theta = 4\\&r = \frac{4}{sen \theta}\\&\\&c) xy=4\\&(r \cos \theta)(r sen \theta) = 4\\&r^2 \cos \theta sen \theta = 4\\&r^2 \frac{sen (2 \theta)}{2} = 4\\&r = \sqrt{\frac{8}{ sen(2 \theta)}}\end{align}$$Las gráficas tomalas a medias, porque no tengo ninguna aplicación que grafique directamente en coordenadas polares :( (para graficar el primer ejercicio, consideré x^2+y^2=2^2)
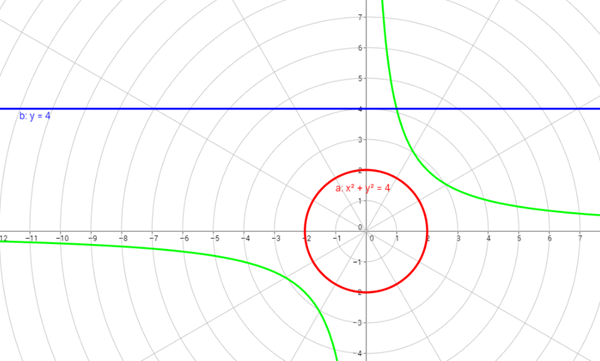
![]() b)
b) c)
c)![]()

