¿Cómo resuelvo esta ecuación de triángulos?
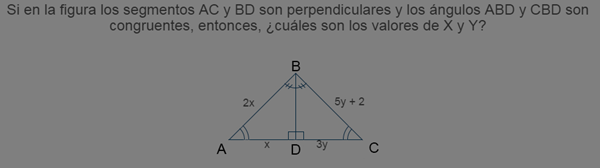
Alguien que por favor sepa como se resuelve este ejercicio y me lo explique llevo demasiado tiempo intentando resolverlo y no he podido.
2 respuestas
Respuesta de Cyrus ...
1
Respuesta
1
