Sólidos de revolución o cascarones cilindricos ejercicio 2

--

--

¡Hola Moropeza!

Hagamos primero la gráfica, no va a ser espectacular, el giro te lo tendrás que imaginar alrededor del eje Y.

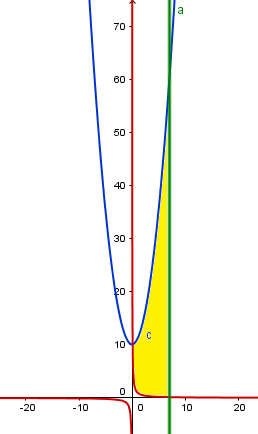
La imagen ha quedado comprimida en anchura pero lo he hecho así para que los ejes tengan la misma proporción. Entonces aunque pueda parecerlo la función roja y azul no se cortan en x=0, vamos a calcular el punto de corte

x^2+10 = 1/x

x^3 + 10x = 1

Aquí se han pasado, no se puede poner una ecuación de grado 3 salvo que se esté estudiando resolución de ecuaciones de grado mayor que dos.

Wolfram Alpha dice que la solución es:

x=0.0999002988054729

Y la fórmula de volumen con los cascarones cilíndricos es

$$\begin{align}&V=2\pi\int_a^b x\,f(x)dx\\&\\&\text{aunque lo correcto sería usar esto}\\&\\&V=2\pi\int_a^b |x\,f(x)|dx\\&\\&\text{Cuando sea entre dos funciones hay que usar}\\&\\&V=2\pi\int_a^b|x(f(x)-g(x)|dx\end{align}$$

Y hay que tener mucho cuidado si las funciones se cortan dentro del intervalo de integración, habrá que dividir la integral en tantos intervalos como haya con posiciónes cambidas de las funciones.

En el ejemplo que nos ocupa creo que no quieren considerar el volumen que generan entre 0 y 0.0999002988054729. El cual daría lugar a una integral impropia pero convergente. Luego consideraré solo el volumen que se genera desde 0.0999002988054729 hasta 7. Además voy a redondear algo ese número.

$$\begin{align}&V=2\pi\int_{0.0999}^7x\left(x^2+10-\frac 1x\right)dx=\\&\\&2\pi\int_{0.0999}^7\left(x^3+10x-1\right)dx=\\&\\&2\pi\left[\frac {x^4}4+5x^2-x  \right]_{0.0999}^7\approx\\&\\&2\pi\left(\frac{2401}{4}+245-7-0.0000249-0.04990005+0.0999  \right)\approx\\&\\&2\pi·838.2999751 \approx 1676.59995\pi\approx\\&\\&5267.194086\\&\\&\end{align}$$

--

--