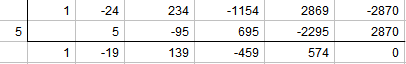Indique el numero de soluciones reales que tiene la siguiente ecuación:

--

--

¡Hola Luis Alberto!

Sé que has querido poner exponentes 5 y 4 pero tienes que escribirlos bien para que se entienda, los exponentes tienen que ir precedidos del signo ^

(x - 5)^5 + (x - 4)^4 = 1

No sé lo que estarás estudiando, eso podría ser importante decirlo.

Vamos a ver si la regla de los signos de Descartes nos puede ayudar. Para ello primero pondremos el polinomio completamente desarrollado

(x-5)^5 + (x-4)^4 - 1=

x^5 - 25x^4 +250x^3 - 1250x^2 + 3125x - 3125 + x^4 - 16x^3 + 96x^2 - 256x +256 -1 =

x^5 - 24x^4 + 234x^3 - 1154x^2 + 2869x - 2870

Hay 5 cambios de signo, luego puede haber 5, 3 ó 1 raíces reales positivas

Si ponemos el polinomio en función de (-x) tendremos

(-x)^5 - 24(-x)^4 + 234(-x)^3 - 1154(-x)^2 + 2869(-x) - 2870=

-x^5 - 24x^4 - 234x^3 - 1154x^2 - 2869x - 2870

No hay ningún cambio de signo, luego no hay raíces negativas.

Luego el polinomio tendrá

a) 5 soluciones reales positivas

b) 3 reales positivas y un par de complejas conjugadas

c) 1 real positiva y dos pares de complejas conjugadas

Esto no ayuda mucho.

Sin embargo si tomamos el polinomio original

(x-5)^5 + (x-4)^4 - 1 = 0

vemos fácilmente que x=5 es una respuesta

(5-5)^5 + (5-4)^4 -1 = 0+1+1=0

Mediante la regla de Ruffini vamos a calcular la división por x-5

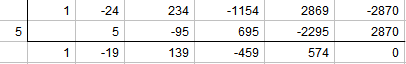
Nos da un polinomio con alternancia de signos y por lo tanto podrá tener 4, 2 ó 0 raíces positivas, no nos sirve de nada.

Otra cosa que podemos deducir es que 5 es la mayor raíz posible.

Ya que si x>=5 tendremos

(x-5)^5 >= 0

(x-4)^4 >= 1

(x-5)^5 + (x-4)^4 -1 >= 0+1-1 = 0

Luego sabiendo que las raíces reales son todas positivas y la mayor es 5 podríamos usar el truco de hacer la gráfica entre 0 y 5 y ver si hay otras raíces. Eso hago con Geogebra acortando mucho el eje Y para que pueda verse

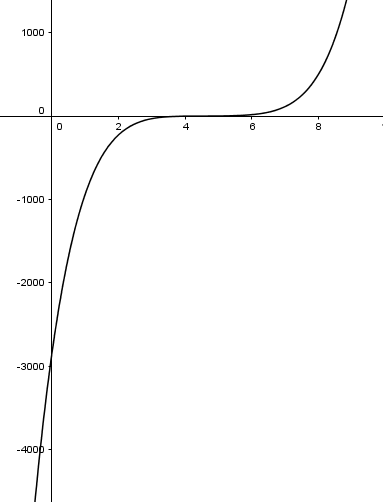
Parece que no haya otra, por si quedan dudas se deja el eje Y a tamaño normal

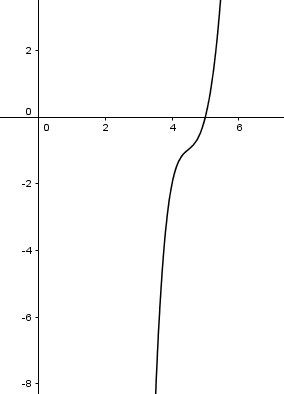
No hay otro corte con el eje X.

Y se puede usar cualquier programa que halle raíces de polinomios, o la página de Wolfram Alpha

http://www.wolframalpha.com/input/?i=%28x-5%29^5%2B%28x-4%29^4-1%3D0 

Y si pinchas el enlace verás que te da las 5 respuestas. La real y las 4 complejas

Luego por lo menos ten por seguro que solo hay una raíz real que es x=5

Ahora bien, si necesitas la resolución puramente teórica yo no puedo hacer más de lo que hice, ya ves qe no ha salido nada sencillo, necesitaría tener el libro o apuntes que estés estudiando.

Saludos.

--

--

Más bien que pinchar en el enlace de Wolfram Alpha tendrás que copiarlo y pegarlo en la barra de direcciones del navegador, esta página tiene fallos con los enlaces a determinadas webs que no los hace clicables.