Area comprendida entre dos curvas...

·

·

¡Hola Gabriela!

Son dos curvas polinómicas de grado 2, eso siginifica que se cortan a lo sumo en dos puntos que serán los limites de integración. Pero lo auténticamente bueno es que no se cortarán en tres puntos, eso significa que no se cruzan en un punto intermedio y por tanto el área entre las dos se calcula en un solo paso. Y esto evita hacer la gráfica.

Calculamos los puntos de corte

3x^2-x-3 = -2x^2+4x+7  

5x^2 - 5x - 10 = 0

x^2 - x - 2 = 0

Si no ves la factorización resuelve la ecuación normalmente

(x-2)(x+1)=0

Luego los puntos de corte son x=-1  y  x=2

Fíjate como la primera parábola tiene forma de U y la segunda al revés, luego en la región que delimitan la segunda es la curva superior y la primera la inferior. Con todo esto el área es:

$$\begin{align}&A=\int_{-1}^2\bigg(-2x^2+4x+7-(3x^2-x-3)\bigg)dx=\\&\\&\int_{-1}^2(-2x^2+4x+7-3x^2+x+3)dx=\\&\\&\int_{-1}^2(-5x^2+5x+10)dx=\\&\\&\left[-\frac{5x^3}{3}+\frac{5x^2}{2}+10x  \right]_{-1}^2=\\&\\&-\frac {40}3+10+20-\frac 53-\frac 52+10 = \\&\\&-\frac {45}3-\frac 52+40=\frac{-90-15+240}{6}=\\&\\&\frac{135}{6}=\frac {45}2=22.5\end{align}$$

:

:

El área comprendida entre dos funciones se calcula como

$$\begin{align}&\int_a^b(f(x)-g(x))dx\end{align}$$

Donde a y b son las abscisas de los puntos de corte y

f(x) es la función que limita por arriba y

g(x) la función que limita por abajo el recinto en cuestión.

No es necesario hacer el dibujo, puedes hacer arbitrariamente una menos la otra y si da negativo coger el valor absoluto.(Si da negativo es que haces f-g)

Calculo de los puntos de corte (resolviendo el sistema):

$$\begin{align}&y=3x^2-x-3\\&y=-2x^2+4x+7\\&3x^2-x-3=-2x^2+4x+7\\&5x^2-5x-10=0\\&x^2-x-2=0\\&\\&x=\frac{-(-1) \pm \sqrt {(-1)^2-4(1(-2)}}{2}=\frac{1 \pm 3}{2}=\\&x_1=2\\&x_2=-1\\&\\&Area= \int_{-1}^2[-2x^2+4x+7-(3x^2-x-3)]dx=\\&\\&\int_{-1}^2(-5x^2+5x+10)dx=\\&\\&\Bigg [\frac{-5x^3}{3}+\frac{5x^2}{2}+10x \Bigg]_{-1}^2=\\&\\&\frac{-5(2)^3}{3}+\frac{5(2)^2}{2}+10(2)- \Big[\frac {-5(-1)^3}{3}+\frac{5(-1)^2}{2}+10(-1) \Big]=\\&\\&\frac{-40}{3}+10+20-\Big(\frac{5}{3}+\frac{5}{2}-10 \Big)=22.5\ \ \ u^2\\&\\&\end{align}$$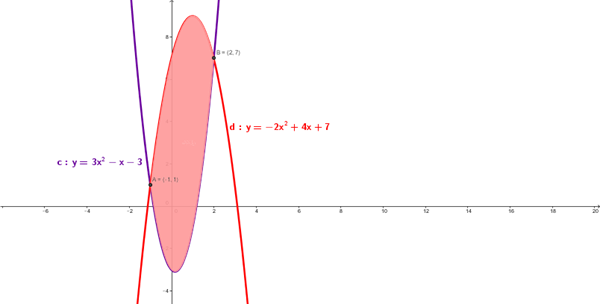

Saludos

:

: