Cual es la ecuación ordinaria de la parábola vertical que abre hacia abajo?

Si los 3 puntos corresponden a los vértices de 3 parábolas distintas, entonces te faltan datos ya que solo tendrías 1 punto para cada parábola y existen infinitas parábolas que pasan por un vértice.

Ej/ sea el punto Z = (0,0), entonces

y = - a x^2

Con a > 0, te da las infinitas ecuaciones de parábolas hacia abajo que pasan por (0,0), simplemente debes ir haciendo variar el valor de "a"

·

·

¡Hola Fabiola!

El vértice y la dirección no son datos suficientes para definir una parábola, habrá toda una familia infinita de parábolas que lo cumplan. Haré el primero y los otros son similares.

H(-3,8)

La parábola será:

f(x) = ax^2+bx+c=0   con a<=0

la coordenada x del vértice es

x=-b/(2a)

-3 =-b/(2a)

6a=b

Luego de momento tenemos la función

f(x) = ax^2 + 6ax + c   con a<=0

Y en el vertice el valor es 8 luego

8 = a·(-3)^2 + 6a(-3) + c

8 =9a - 18a + c

c = 8 + 9a

Luego la familia de parábolas es

f(x) = ax^2 + 6ax + 8 + 9a   con a<=0

Se que esa forma de espresarlo no es muy popular, luego vamos a hacerlo de otra

$$\begin{align}&f(x) = -k^2x^2-6k^2x -9k^2+8  \end{align}$$

Con esto ya no hay problema, cualquiera que sea el valor de k te da una parábola que cumple eso.

Por ejemplo tomando k=1 tendremos

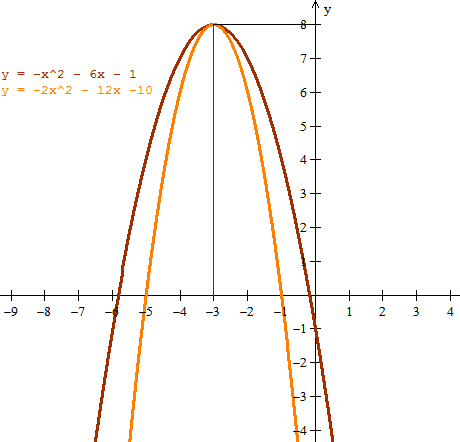
f(x) = -x^2 - 6x - 1

Para k=raiz(2) tendremos

f(x) = -2x^2 - 12x -10

Aquí tienes las gráficas:

Y eso es todo, espero que te sirva y lo hayas entendido. Si no puedes hacer los otros dos ejercicios manda sendas preguntas con ellos. NO olvides puntuar

Saludos.

:

: