Como puedo sacar los vértices de un triangulo si los puntos medios de los lados son a (-2,2) b(8,4) c (4,10) y la razón es de 1
Ya que es un tema un poco complicado para mi
2 respuestas
Que la razón sea 1 no se a que se refiere, pero para mí la resolución es la siguiente. Te dejo la imagen porque no tengo ganas de hacer muchas cuentas :-)
Básicamente lo que hice fue:
1. Primero imaginate el caso inverso, vos tenés el triángulo y definís el triángulo interior marcando los puntos medios de cada lado. Verás que te queda otro triángulo con lados paralelos al triángulo original.
2. Con el punto anterior en mente, creé un triángulo con los puntos dados.
3. Tiré paralelas a cada lado, que pasen por el vértice que quedaba libre
4. Donde se cortan estas 3 nuevas rectas generadas, tenés los puntos de tu triángulo
Analíticamente también se puede hacer pero son muchas más cuentas; por ejemplo, definamos la recta B'C' del gráfico que te dejo.
Sabemos que la pendiente es la misma que BC luego
y = mx + b
m = (4-10) / (8-4) = -1.5
y = -1.5x + b
y sabemos que pasa por el punto A (-2,2), así que
2 = -1.5 (-2) + b
b = -1
O sea que la recta B'C' es y = -1.5x - 1
De la misma forma se pueden calcular A'B' y A'C', una vez que tienes las 3 rectas las igualas para ver donde se cortan. Si quieres seguir con la parte analítica y no te sale, repregunta pero intenta resolverlo primero para ver hasta donde llegas.
Te dejo la imagen
·
·
¡Hola Jimena!
Interesante la forma de hacerlo de Gustavo por semejanza de triángulos, pero es muy probable que los estéis haciendo de esa forma. Voy a hacerlo de forma directa.
El punto medio de un lado de un triángulo se obtiene haciendo la semisuma coordenada a coordenada de las coordenadas de los vértices, es decir, si los vértices son (a, b) y (c, d) el punto medio es
[(a,b)+(c,d)] / 2 = ((a+c)/2 , (b+d)/2)
El triángulo tiene tres vértices, luego tendremos 6 incógnitas, las de los puntos
(a,b), (c,d) y (e,f)
Pongamos que (-2,2) es el punto medio del lado entre (a, b) y (c, d) de acuerdo con la fórmula que ya pusimos arriba tenemos
(a+c)/2=-2 ==> a+c=-4
(b+d)/2= 2 ==> b+d=4
Ahora sea (8,4) el punto medio del lado entre (c, d) y (e, f). Aligerando y pasando ya el 2 del denominador a la derecha tendremos
c+e=16
d+f=8
Y para el punto medio (4,10) entre (a,b) y (e,f) tenemos
a+e=8
b+f=20
Tenemos 6 ecuaciones, pero las incógnitas van en dos grupos de tres, el primero es:
1) a+c=-4
2) c+e=16
3) a+e=8
Vamos a sumar la primera con la segunda y le restaremos la tercera
a+c+c+e-a-e = -4+16-8
2c = 4
c=2
y ya con esto
a+2=-4 ==> a=-6
2+e=16 ==> e=14
·
Y el otro grupo de ecuaciones es
4) b+d=4
5) d+f=8
6) b+f=20
Lo mismo de antes, sumo primera con segunda y resto la tercera
b+d+d+f-b-f = 4+8-20
2d = -8
d=-4
y se calculan las otras dos
b-4 = 4 ==> b=8
-4+f=8 ==> f=12
Luego los vértices del triángulo son
D=(a,b) = (-6, 8)
E=(c,d) = (2, -4)
F=(e,f) = (14, 12)
Es conveniente hacer la gráfica para comprobarlo.
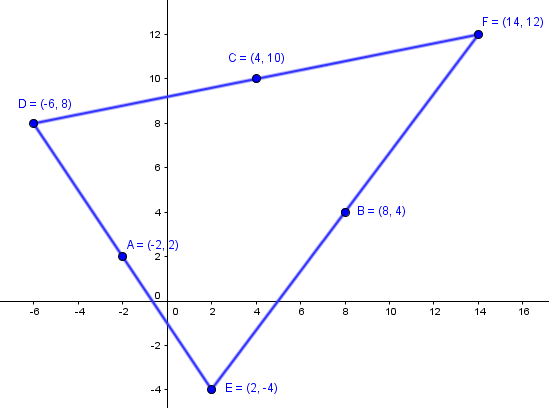
Y la comprobación visual no deja lugar a la duda de que está bien.
Cuando al principio decía "pero es muy probable que los estéis haciendo de esa forma" quería decir lo contrario "pero es muy probable que NO los estéis haciendo de esa forma"
Saludos.
:
: