Tengo dudas respecto a Inecuaciones y Desigualdades parte II ejercicio (5c)
Amigos favor su ayuda en resolver el ejercicio
En su pregunta (c)
(c) Resolver la inecuación para valores negativos de a.
·
·
¡Hola Marco!
Si lo quieres hacer con deducciones lógicas considerando casos según los signos de los factores que van de un lado a otro y cambiando o no cambiando el sentido de la desigualdad te vas a volver loco como me ha sucedido a mí. Por eso te planteo resolverlo como te voy a mostrar.
$$\begin{align}&\frac{x^2}{x-a}\ge x+1\\&\\&\frac{x^2}{x-a}-(x+1)\ge 0\\&\\&\frac{x^2-x^2+x+ax-a}{x-a}\ge 0\\&\\&\frac{x+ax-a}{x-a}\ge 0\\&\\&\frac{(x-a)+ax}{x-a}\ge 0\\&\\&1+\frac{ax}{x-a}\ge 0\\&\\&\text{llamemos }\;\;f(x)=1+\frac{ax}{x-a}\\&\\&\text{f es continua en }\mathbb R-\{a\}\\&\\&\lim_{x\to \pm\infty}f(x) = 1+a\\&\\&\lim_{x\to a^-}f(x) = 1+\frac{a^2}{-0}=-\infty\\&\\&\lim_{x\to a^+}f(x)= 1+\frac{a^2}{+0}=+\infty\\&\\&f'(x)=\frac{a(x-a)-ax}{(x-a)^2}=-\frac{a^2}{(x-a)^2}\lt0\\&\\&\text{luego f es siempre dececiente} \end{align}$$Luego la función es así, en -infinito tiende a 1+a, luego desciende hasta -infinito en x=a se da la vuelta en ese mismo punto tendiendo a infinito y vuelve a descender hasta 1+a en cuando x tiende a infinito
El corte con el eje X es
x+ax-a = 0
x(1+a) = a
x=a/(1+a)
Entonces hay tres casos
1) Si -1<a<0
Entonces el límite en -infinito es
a+1>0
Luego corta al eje antes de x=a donde vale -infinito
Y después se hace positiva y ya no lo vuelve a cortar. Luego la función es positiva y es respuesta de la inecuación en:
(-inf, a/(1+a)) U (a, +inf)
·
2) a=-1
La asíntota horizontal es 0, la función no corta al eje POR nunca y es positiva a la derecha de la asíntota vertical. La solución es
(-1, +infinito)
3) -infinito < a < -1
Entonces a-1<0 y a la izquierda de la asíntota vertical no está el corte, lo está a la derecha, la franja positiva de f y solución es:
(a, (a/(1+a))
Y la gráfica te ayudará a visualizarlo y comprobarlo.
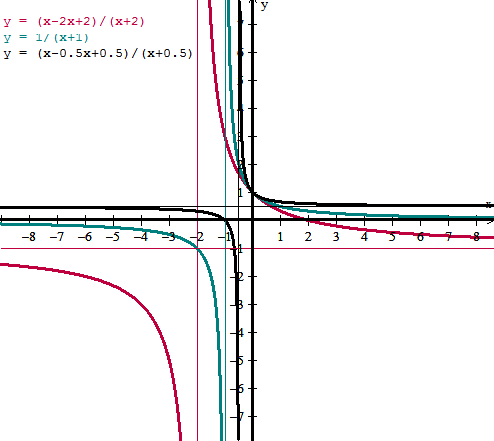
Tienes tres funciones, la negra con a=-0.5, corresponde al caso 1 y como puedes ver la solución es
(-inf, -0.5/(1-0.5)) U (-0.5, +inf) =
(-inf, -1) U(-0.5, +inf)
La verde es la de a=-1, corresponde al caso 2 y la solución es
(-1, +inf)
Y la roja con a=-2 corresponde al caso 3 y la solución
(-2, -2/(1-2)) = (-2, 2)
:
:
