Hallar la ecuación de la circunferencia

Sea la circunferencia de centro C(a, b) y radio r:

(x-a)^2+(y-b)^2=r^2

Si pasa por los puntos A y B, al sustituir ha de cumplir la ecuación. Luego sustituyéndolos:

A(7,-9):

$$\begin{align}&(7-a)^2+(-9-b)^2=r^2\\&\\&B(3,-1)\\&(3-a)^2+(-1-b)^2=r^2\\&\\&desarrollándolas:\\&9-6a+a^2+1+b^2+2b=r^2\\&49-14a+a^2+81+b^2+18b=r^2\\&\\&restándolas:\\&-40+8a-80-16b=0\\&8a-16b=120\\&simplificándola:\\&a-2b=15\end{align}$$

Si la recta es tangente a la circunferencia, el vector CB será perpendicular al vector de dirección de la recta, luego su producto escalar dará 0:

\v

$$\begin{align}&\vec{CB}=B-C=(3,-1)-(a,b)=(3-a,-1-b)\\&\\&\vec{d}=(-1,1)\\&\\&\vec{CB}·\vec{d}=0\\&(3-a,-1-b)·(1,1)=0\\&3-a-1-b=0\\&2=a+b\\&\\&Resolviendo \ sistema\\&a-2b=15\\&-a-b=-2\\&\\&sumandolas\\&-3b=13 \Rightarrow b=-\frac{13}{3} \Rightarrow a=2-b=\frac{19}{3}\\&\\&º centro \ \ C=(\frac{19}{3},- \frac{13}{3})\\&\\&r=| \vec{CB}|\\&\vec{CB}=(3-\frac{19}{3},-1+\frac{13}{3})=(-\frac{10}{3},\frac{10}{3})\\&r=| \vec{CB}|=\sqrt{(\frac{10}{3})^2+\frac{10}{3})^2}=\sqrt{\frac{200}{9}}=\frac{10}{3} \sqrt 2\\&\\&circunf.\\&\\&(x-\frac{19}{3})^2+(y+\frac{13}{3})^2=\frac{200}{9}\end{align}$$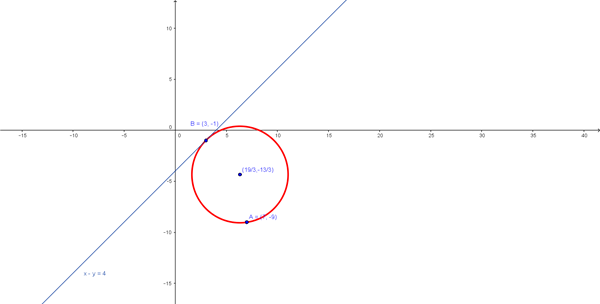

SAludos

;

;