Tengo una duda de Dominio calculo diferencial
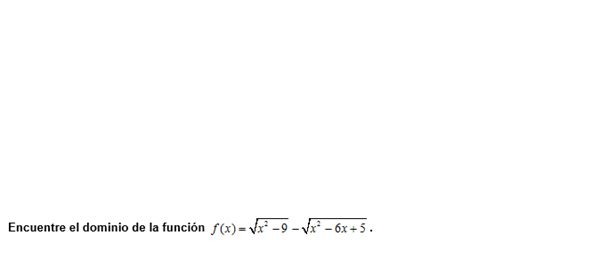
Me podrian ayudar por favor ya que no le entiendo muy bien
1 Respuesta
Respuesta
1
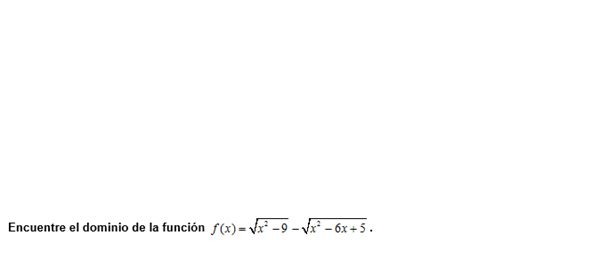
Me podrian ayudar por favor ya que no le entiendo muy bien
