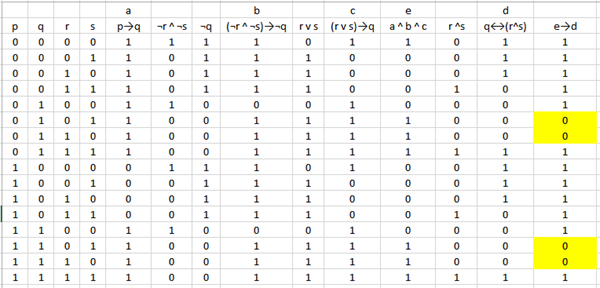
Realicen el planteamiento y la solución del siguiente problema de Lógica Proposicional:
- Si Soraida estudia Ingeniería Electrónica, entonces participará en la convocatoria laboral de una empresa de equipos tecnológicos. Pero, no participará en la convocatoria laboral de una empresa de equipos tecnológicos, si Soraida reprobó el curso de Telemática y no aprobó el curso de Microcontroladores. Si Soraida no reprobó el curso de Telemática o aprobó el curso de Microcontroladores, entonces participará en la convocatoria laboral de una empresa de equipos tecnológicos. Por lo tanto, participará en la convocatoria laboral de una empresa de equipos tecnológicos si y solo si evidencia un promedio de 4,3 en todos sus estudios.
1 Respuesta
Respuesta de Valero Angel Serrano Mercadal
1