Quiero resolver teoremas de Calculo

·

·

¡Hola Julio!

No en todos los sitios te van a poner el mismo enunciado, y en algunos se habla del primer y segundo teorema, te pongo lo que dice la wikipedia:

Primer teorema fundamental del cálculo:

Dada una función f integrable sobre el intervalo 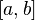, definimos F sobre 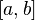por 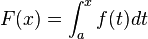. Si f es continua en 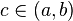, entonces F es derivable en y F'(c) = f(c).

·

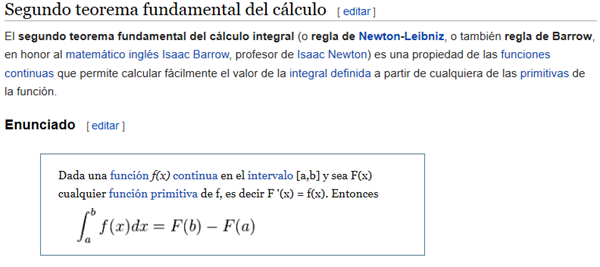
Y el segundo:

Dada una función f(x) continua en el intervalo [a,b] y sea F(x) cualquier función primitiva de f, es decir F '(x) = f(x). Entonces

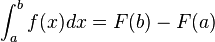
Lo que diga tu libro o apuntes es lo que debe prevalecer.

Las ventajas son sobre todo a la hora de realizar integrales, qe mediantes sumas de Riemann por ejemplo serían harto difíciles o cuanto menos muy pesadas de realizar.

En la integral se han debido equivocar, tendría que coincidir la variable y la diferencial. Tal como está escrito la integral es un constante C, pero se supone que debería ser esta:

$$\begin{align}&\int \frac{y^{\frac 72}+y^{\frac 52}-y^{\frac 14}}{y^2}dy=\\&\\&\int \left(y^{\frac 32}+y^{\frac 12}- y^{-\frac 74} \right)dy=\\&\\&\frac{y^{\frac 52}}{\frac 52}+\frac{y^{\frac 32}}{\frac 32}-\frac{y^{-\frac 34}}{-\frac 34}+C=\\&\\&\frac 25y^{\frac 52}+\frac 23y^{\frac 32}+\frac 43y^{-\frac 34}+C\end{align}$$

:

:

¡Por Dios que horror!

Yo solo copié y pegué dos cuadraditos con los enunciados de los teoremas y aquí ha aparecido la mitad de la Wikipedia. Voy a poner de nuevo los teoremas de otra forma:

Saludos.

:

:

¡Que horror!

Yo solo copié y pegué los cuadraditos de los teoremas y ha aparecido aquí toda la página de la Wikipedia. Voy a hacerlo con recortes de la pantalla para que solo salga lo que yo quiero:

Y eso es todo, saludos.

:

: