Operaciones básicas con polinomios. Cuáles son los resultados siguientes ?
Ana encontró un cartón rectangular en su casa y decide reciclarla realizando con él una caja sin tapa para guardar en ella los cables y accesorios de su celular. El cartón mide 40 por 20 centímetros y la construcción se realizará recortando cuatro cuadrados iguales en cada una de las esquinas. Escribe las expresiones algebraicas de la Superficie y el Volumen de la caja en función del lado del cuadrado.
La siguiente imagen muestra los cortes que realizará Ana en el cartón para hacer la caja
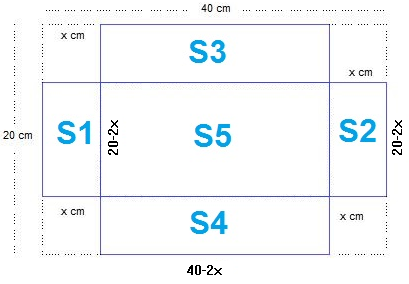
Para expresar la Superficie de la caja, debemos identificar primero que al recortar los cuadros de las esquinas se forman cinco rectángulos, recuerda que la Superficie de un rectángulo se obtiene al multiplicar la base por la altura, es decir S = bh.
En este caso tenemos cinco rectángulos por lo tanto debemos obtener la expresión para cada uno, para la Superficie 1 (S1) la base es x y la altura es 20 – 2x, entonces la expresión de la Superficie 1 sería:
S1 = x (20 – 2x)
Expresa algebraicamente las otras cuatro superficies:
S2 =
S3 =
S4 =
S5 =
La superficie total de la caja será S = S1 + S2 + S3 + S4 + S5
Escribe la expresión de la Superficie sumando las cinco expresiones obtenidas anteriormente
S =
Para calcular el Volumen de la caja, recordemos que el Volumen es Superficie de la base por la altura, en este caso la Superficie de la base es S5 y la altura x.
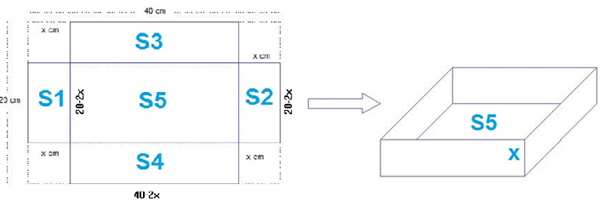
Expresa la expresión algebraica que representa el volumen de la caja.
V = (S5)(x)
V =
Para dar respuesta a las siguientes preguntas considera las expresiones algebraicas que elaboraste:
a) Encuentra el volumen de la caja su altura es de 5 centímetros __________________________
b) Encuentra la superficie de la caja si la altura es de 3 cm
c) Si necesitamos que la superficie de la caja sea de 784 cm2 ¿Cuánto debe valer la altura de la caja? __________________________
d) Si la altura de la caja es de cero cm., calcula la superficie total y el volumen de la caja. __________________________
e) Considera las superficies S1, S2, S3, S4 y S5, imagina que le pondrás un forro en la base y otro en las paredes laterales, el forro para la base cuesta $1.2 cada cm2 y el forro para las paredes laterales cuesta $1.5 cada cm2, si la altura de la caja es de 3 cm, calcula cuánto dinero se gastará en forrar todo el interior de la caja. __________________________
f) Recuerda que 1L = 1000 cm3, calcula cuántos litros le caben a la caja si su altura es de 7 cm __________________________
g) Recuerda que 1L = 1000 cm3, calcula cuántos litros le caben a la caja si su altura es de 8 cm __________________________
Desarrollo:
Solución:
Intenta resolverla, si no como vas a aprender.
3 respuestas más de otros expertos
''
''
¡Hola Rocio!
Fíjate que S1=S2 y S3=S4 ya que tienen idénticas medidas de base y altura.
Luego
S = 2S1 + 2S3 + S5 =
2x(20-2x) + 2x(40-2x) + (40-2x)(20-2x)=
40x - 4x^2 + 80x - 4x^2 + 800 - 80x - 40x +4x^2 =
x^2(-4-4+4) + x(40+80-80-40) + 800 =
-4x^2 + 0x +800
S = 800-4x^2 cm^2
·
Y la expresión del volumen es el producto de las tres dimensiones que llamaremos anchura, profundidad y altura.
V = (40-2x)(20-2x)x = (800 - 80x - 40x -4x^2)x = (800 - 120x - 4x^2)x =
800x - 120x^2- 4x^3
Fíjate que en realidad te he dado tres fórmulas, porque seguro si qte quedas en una el profesor dirá que no has trabajado suficiente, estás son las tres
V=(40-2x)(20-2x)x
V=(800-120x-4x^2)x
V= 800 - 120x^2 - 4x^3
A la gente le suele gustar más la tercera, pero la mejor es la primera, y aun la vamos a mejorar un poquito
V = (40-2x)(20-2x)x = 2(20-x)·2(10-x)·x
V = 4x(20-x)(10-x)
Esta es la expresión que requiere menos operaciones y más sencillas
a)
Sustituyendo x=5 en la última fórmula del volumen tenemos
V=4·5(20-5)(10-5) = 20·15·5 = 1500 cm^3
b)
En la fórmula que habíamos encontrado para la superficie sustituimos x=2
S = 800 - 4·3^2 = 800 - 4·9 = 800-36 = 764 cm^2
c)
Tendremos que poner 784 en el lado izquierdo de la fórmula y despejar x
784 = 800 - 4x^2
4x^2 = 800 - 784 = 16
x^2 = 16/4 = 4
x = raíz(4) = 2 cm
d)
Las calculamos a partir de las fórmulas
S=800-4x^2 = 800 - 4·0^2 = 800 - 0 = 800 cm^2
V= 4·0·(20-0)·(10-0) = 0
nada más que un factor es 0 el resultado es 0
e)
Si la altura de la caja la superficie total es
800 - 4·3^2 = 800 - 4·9 = 800 - 36 = 764 cm^2
La superficie de la base es
S5 = (40-2·3)·(20-2·3) = (40-6)(20-6) = 34·14 = 476 cm^2
Luego la superficie lateral es
S1+S2+S3+S4 = 764 - 476 = 288 cm^2
Y el precio será
PVP = 476 · $1.2 + 288 · $1.5 = $571.20 + $432 = $1003.20
f)
Calculamos el volumen para x=7
V=4x(20-x)(10-x) = 4·7·(20-7)(10-7) = 28·13·3 = 1092 cm^3
La capacidad en litros se obtiene dividiendo entre 1000
1092 / 1000 = 1.092 litros
g)
Y cuando x=8 el volumen es
V=4·8(20-8)(10-8) = 32·12·2 = 768 cm^3 = 0.768 litros
' '
' '
·
·
¡Hola de nuevo!
Espero te hayas dado cuenta que había un fallo y no te haya afectado.
Cuando decía:
V=(40-2x)(20-2x)x
V=(800-120x-4x^2)x
V= 800 - 120x^2 - 4x^3
en el último paso me equivoqué en un signo y es
V = 800 - 120x^2 + 4x^3
Esto no afecta al resto de apartados ya que los cñaculos no los hice con esa fórmula sino con
V = 4x(20-x)(10-x)
Perdón por el fallo.
Saludos.
:
:
Aprovecho para corregir un fallo que tuve el la corrección de un fallo inicial. Si es que en este ejercicio no he estado inspirado. La fórmula del volumen definitivamente es
V=(40-2x)(20-2x)x
V=(800-120x+4x^2)x
V= 800x - 120x^2 + 4x^3
·
Y ahora contesto aquí a Jorge López.
Dice que no entiende lo de
V = 4x(20-x)(10-x)
No hay que entenderla, es una simplificación que hice yo, esa formúla viene de esta otra
V=(40-2x)(20-2x)x
Lo que pasa es que a mí me gusta manejar números más pequeños para poder hacer las multiplicaciones mentalemente con menos esfuerzo, por eso saco factores comunes
V = (40-2x)(20-2x)x = [2(20-x)]·[2(10-x)]· x
y ahora reordenando factores
V = 2·2·x(20-x)(10-x) = 4x(20-x)(10-x)
Era simplemente porque yo prefiero hacer esa operación a la inicial.
Y por supuesto la que de ninguna manera me gustaría hacer es:
V = 800x - 120x^2 + 4x^3
Aunque sé que hay gente que es la que usaría.
Y eso es todo, saludos.
:
:
No se si van todos al mismo colegio o a los profesores se les acabaron las ideas y dan todos el mismo ejercicio pues esta pregunta ya la hemos respondido al menos 5 veces, jaja
Te dejo un link a una de estas respuestas. No olvides votar allá y acá a todos los expertos
Tengo una duda en el procedimiento le entiendo perfectamente solo que me perdí en esta parte.
V=4x(20-x)(10-x)
El 4x representa las 4 paredes creo entender
Este (20-x)(20-x) 20 por el largo de S1 o S2 y x es el valor 7 de altura
Y el 10 no se que es lo que representa, segun mi criterio falta el largo de 40 porque si ya incluimos S1 y S2 con 20 de largo, falta el S3 y S4 que seria 40-X
V=4x(20-x)(40-x)
por algo se busca ayuda , no entemos el procedimiento..voto negativ - Anónimo