Como hallar Df en el siguiente ejercicio?
Sea f(x)= 1/x - 1/x2^ + 2
1) Hallar Df y calcular lim+-∞f(x) y lim 0+-f(x)
2) Hallar los puntos de corte de ef con OX y OY
3) Estudiar las variaciones de f y trazar la curva.
1 Respuesta
Respuesta de Lucas m
2
Entiendo esto:
$$\begin{align}&y=\frac{1}{x}-\frac{1}{x^2}+2=\frac{x-1+2x^2}{x^2}\\&\\&Dom =\mathbb R-\{0\}\\&\\&\lim_{x\to 0}\frac{x-1+2x^2}{x^2}=\frac{-1}{0}=\infty\\&Asintota \ Vertical \ \ x=0 \ \ (eje Y)\\&\\&\lim_{x\to + \infty}\frac{x-1+2x^2}{x^2}=\lim_{x\to \infty}\frac{2x^2}{x^2}=2\\&\\&\lim_{x\to - \infty}\frac{x-1+2x^2}{x^2}=\lim_{x\to - \infty}\frac{2x^2}{x^2}=2\\&Asíntota \ Horizontal\ y=2\\&\\&crecimiento:\\&\\&y'=\frac{(4x+1)x^2-(2x^2+x-1)(2x)}{x^4}=\\&\\&simplificando \ una \ x\\&\\&=\frac{(4x+1)x-(2x^2+x-1)(2)}{x^3}=\frac{4x^2+x-4x^2-2x+2}{x^3}=\\&\\&=\frac{2-x}{x^3}\\&\\&puntos \ críticos \ \Rightarrow y'=0\\&\\&\frac{2-x}{x^3}=0\\&\\&2-x=0\\&\\&x=2\\&\\&Intervalos \ crecimiento:\\&\\&(-\infty,0) \Longrightarrow y(-10)'=\frac{2-(-10)}{(-10)^3}=\frac{+}{-}=- \Rightarrow \ Decreciente\\&\\&(0,2) \Longrightarrow y(1)'=\frac{2-1}{1}=+ \Rightarrow creciente\\&\\&(2,+\infty) \Longrightarrow y(10)'=\frac{2-10}{10^3}=\frac{-}{+}=- \Rightarrow \ Decreciente\\&\\&\\&\Longrightarrow x=2 \ es \ Máximo \ relativo\\&\\&f(2)=\frac{2(2)^2+2-1}{2^2}=\frac{9}{4}=2.25\\&Maximo (2,\frac{9}{4})\\&\\&\\&\end{align}$$Graficando:
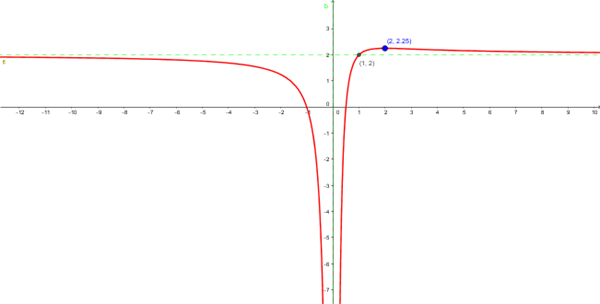
Saludos
;
;
