Ejercicio 2. Un alambre de 150 cm se corta para formar un cuadrado y un triángulo equilátero

Primero dejo una imagen con lo que entiendo que es la figura

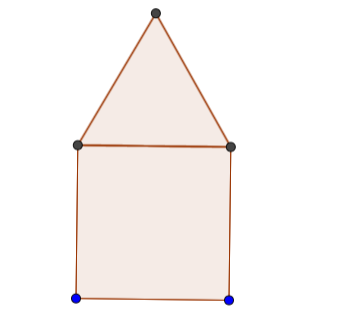
Tenemos 6 lados (ya que comparten 1) y se quiere maximizar el área, pero para esto primero debemos calcular la altura del triángulo

$$\begin{align}&altura \ triángulo = h\\&Lado = L\\&sen 60° = \frac{h}{L}  \Rightarrow h = L sen60° = L \frac{\sqrt 3}{2}\\&\text{Ahora las condiciones del problema}\\&Area = L^2 + L \ L \frac{\sqrt 3}{2} \frac{1}{2} = L^2(1+\frac{\sqrt 3}{4})\\&Condición: 150 = 6L\\&\text{Iba a plantear Lagrange, pero creo que queda 1 sola variable que es L y no hay nada que maximizar y queda}\\&L = \frac{150}{6} = 25\\&Reemplazo \ en \ el\ área:\\&A = 25^2(1+\frac{\sqrt 3}{4})=895,6329 cm^2\end{align}$$

No hay análisis que hacer pues estoy usando todo el alambre y cualquier otra condición hará que el área total sea menor...estimo que debe haber algo mal en el enunciado o interpreté mal el enunciado, ya que me parece raro que haya salido directo...