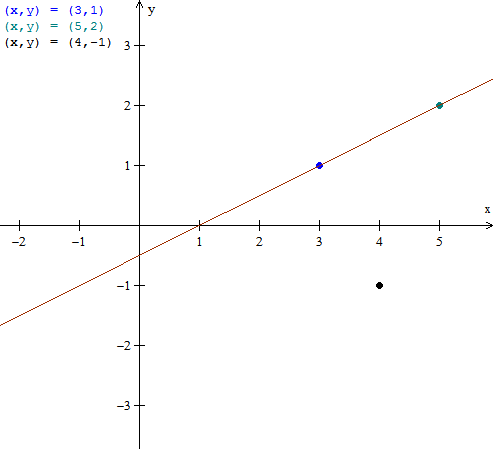Como verificar si A,B y C son alineados?
Sean A, B y C de afijos;
A= 3+i
B= 5+2i
C= 4-i
•Verificar si A, B y C son alineados.
1 respuesta
Respuesta de Valero Angel Serrano Mercadal
1
·
·
¡Hola Sía!
Por supuesto sería calcular la ecuación de la recta definida por dos de ellos y ver que el otro punto pertenece a ella. Pero se puede ahacer un poco más corto. Voy a hacer la teoría de rectas en R2, luego esto se pasa a números complejps de manera trivial.
$$\begin{align}&\text{Sean 3 puntos} \\&A(x_1,y_1)\\&B(x_2,y_2)\\&C(x_3,y_3)\\&\\&\text{la recta definida por A y B sería}\\&\\&\frac{x-x_1}{x_2-x_1}= \frac{y-y_1}{y_2-y_1}\\&\\&\text{si C estuviese en esa recta se cumpliría}\\&\\&\frac{x_3-x_1}{x_2-x_1}= \frac{y_3-y_1}{y_2-y_1}\\&\\&\text{Luego probemos eso, haciendo }x_i\text{ las partes reales}\\&\text{y }y_i \text{ las complejas}\\&A=3+i\\&B=5+2i\\&C=4-i\\&\\&\frac{4-3}{5-3}=\frac{-1-1}{2-1}\\&\\&\frac{1}{2}=\frac {-2}{1}\\&\\&1=-4\quad falso\\&\\&\text{luego no está alineados}\end{align}$$Y la prueba la tienes aquí:
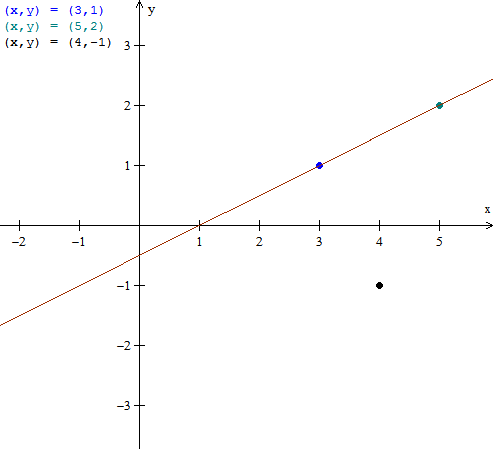
Y eso es todo, saludos.
·
·
