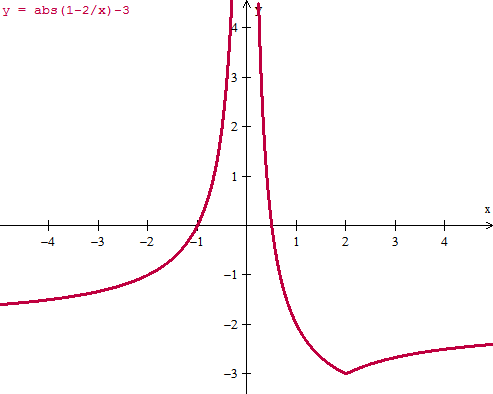
Cómo se resuelven inecuaciones con valor absoluto
I1-2/xI mayor igual que 3
I :son las barras de valor absoluto
2 Respuestas
Respuesta de Valero Angel Serrano Mercadal
1
·
·
¡Hola Rodrigo!
Una ecuación con valor absoluto equivale a dos sin valor absoluto, las llamaremos i) y ii)
$$\begin{align}&\bigg|1-\frac 2x\bigg|\ge 3\\&\\&i)\quad 1-\frac 2x\ge3\\&\\&-\frac 2x\ge2\\&\\&\text{Si x fuera positivo sería imposible, luego debe}\\&\text{ser negativo y al pasar al otro lado cambia el sentido}\\&\\&-2 \le 2x\\&\\&x\ge-1\\&\\&\\&ii)\quad 1 -\frac 2x \le-3\\&\\&-\frac 2x\le-4\\&\\&\text{multiplicamos por -1 y cambia el sentido}\\&\\&\frac 2x\ge4\\&\\&\text{Si x fuera negativo sería imposible, luego}\\&\text{pasa al otro lado manteniéndose el sentido}\\&\\&2 \ge4x\\&\\&x\le \frac 12\\&\\&\text{Uniendo las dos respestas tenemos}\\&\\&-1 \le x\le \frac 12\\&\\&\text{Esa es la solución, o si lo prefieres}\\&\\&x\in \left[-1,\; \frac 12\right]\\&\end{align}$$Por si acaso lo comprobamos.
Está bien, donde esta función es positiva se cumple la inecuación.
:
:
Buena explicación.Sólo te falto quitar el cero a tu solución. Saludos
¡Ah, es verdad! El conjunto solución es:
$$\begin{align}&S=[1,0)\cup\left(0,\frac 12\right]\end{align}$$
Perdón:
$$\begin{align}&S=[-1,0)\cup\left(0,\frac 12\right]\end{align}$$
Respuesta
-1
Si entiendo bien la expresión que pusiste
$$\begin{align}&\bigg | 1 - \frac{2}{x} \bigg | \ge 3\\&\bigg | \frac{x-2}{x} \bigg | \ge 3\\&\text{Lo primero que vemos es que no está definida en x=0, ahora tenemos que separar varios casos}\\&Caso \ 1: x \in (-\infty,0) \text{ (la fracción es >0 y podemos sacar las barras de absoluto directamente):}\\&\frac{x-2}{x} \ge 3\\&{x-2} \le 3x \text{ (Doy vuelta la igualdad porque x <0)}\\&-2 \le 3x -x\\&-2 \le 2x\\&-1 \le x \therefore x \in [-1, 0)\\&Caso\ 2: x \in (0,2) \text{ (la fracción es <0 y para sacar el absoluto multiplicamos por -1):}\\&-\frac{x-2}{x} \ge 3\\&\frac{x-2}{x} \le3\\&x-2 \le 3x\\&-2 \le 2x\\&-1 \le x \text{ pero como x está en (0,2), no hay soluciones en este intervalo}\\&Caso \ 3: x \in [2,+\infty) \text{ (la fracción es >0 y podemos sacar la barra de absoluto directamente):}\\&\frac{x-2}{x} \ge 3\\&x-2 \ge 3x\\&-2 \ge 2x\\&-1\ge x \therefore \text{ tampoco hay solución en este intervalo}\\&\text{Por lo tanto las soluciones son:}\\&x \in [-1,0)\end{align}$$
0 no puede ser según el CVA 2/0 no existe
Si mirás la primer línea que escribí, el cero lo estoy dejando fuera (ya que digo que no está definida). Por otro lado, al poner el paréntesis en el intervalo justamente lo que significa es que ese valor NO está definido.