Utilizando la PRIMERA parte del Teorema fundamental del cálculo (TFC), calcular lo siguiente
Espero me puedan ayudar con estos casos.
Si es necesario dividirlo en varias preguntas lo hago.
Utilizando la PRIMERA parte del Teorema fundamental del cálculo (TFC), calcular lo siguiente
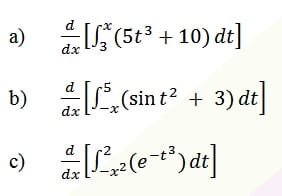
3 respuestas
Respuesta de Jose Otero
1
Respuesta de Lucas m
1
Respuesta de Valero Angel Serrano Mercadal
1
