Como demostrar los siguientes ejercicios?
Demostrar que;
a) cos (a+b)=cos a cos b - sen a sen b
b) cos^2 a= cos^2a+1/2
2 respuestas
Respecto al primer ejercicio no me voy a poner a descubrir el agua caliente, además que esta página es muy mala para incluir textos y gráficos, así que te dejo un link donde está muy "fácil" explicado
Respecto al ejercicio b, confirma la expresión con paréntesis, ya que la expresión así como está tiene varias interpretaciones. Por ejemplo
cos^2 (a) = cos^2(a) + 1/2
o
cos^2(a) = cos^2 (a+1/2)
Que claramente ninguna de estas dos expresiones es verdadera (basta hacer a=0 y verificar que no es cierto)
Es por esto que te pido que confirmes la expresión con paréntesis.
;)
;)
Hola Sia!
Para demostrar la primera fórmula hay diferentes métodos, según el punto de partida
(Vectores, a partir del cos(a-b), utilizando trigonometría básica)
Una demostración usando trigonometría básica es a partir de la siguiente construcción:
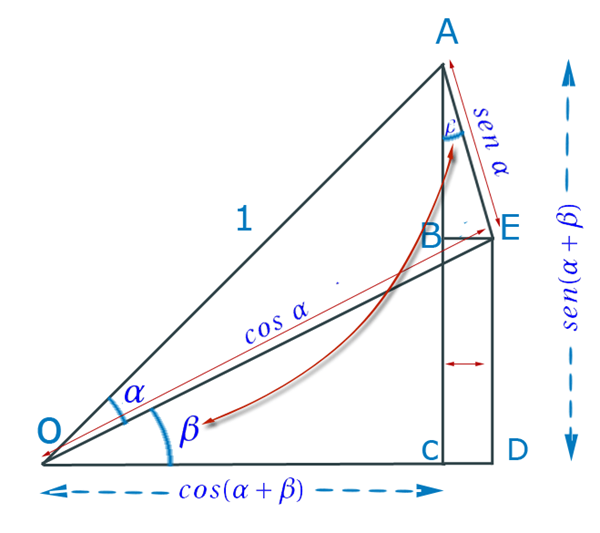
Hemos construido tres triángulos rectángulos: con OA=1
El OAC con ángulo recto en C
El AOE con ángulo recto en E
El OED con ángulo recto en D
Y a parte al trazar la proyección del vértice E en C (B) tenemos el triángulo rectángulo
ABE
Por comodidad los ángulos alpha=a y beta=b
En el triángulo AOE:
AO=1
OE=AO·cosa=1·cosa=cosa
AE=AO·sen a=1·sena=sena
En el triángulo. rectángulo OED
OD=OE·cosb=cosa·cosb
ED=OE·senb=cosa·senb
En el triángulo rectángulo AOC:
OC=AO·cos(a+b)=1·cos(a+b)=cos(a+b) (*)
A parte observando los segmentos se cumple que
OC=OD-CD=cosacosb-CD (**)
Para obtener CD tenemos que ir al triángulo pequeño ABE y observar que
EA es perpendicular a OE y AB perpendicular a OD : lados perpendiculares de un ángulo determinan ángulos iguales, luego el ángulo BAE=EOD=b
luego CD=BE=AE·senb=sena·senb
Luego sustituyendo en (**) OC=coscosb-senasenb
Igualando (*) y (**)
cos(a+b)=cosacosb-senasenb (C.Q.D.)
C.Q.D. como queríamos demostrar
Manda la otra en otra pregunta
Saludos
;)
;)