Como demostrar que los puntos A,B,C y D pertenecen a la misma circunferencia!?

;)

Hola Sia!

$$\begin{align}&\frac{C-A}{D-A}=\frac{2i-(-1+i)}{2-2i-(-1+i)}=\frac{1+i}{3-3i}=(*)\\&\\&|1+i|=\sqrt {1^1+1^2}=\sqrt 2\\&tan \alpha=1 \Rightarrow \alpha =45º\\&\\&|3-3i|=\sqrt {3^2+3^2}=\sqrt {18}=3 \sqrt 2\\&\\&tan \beta=\frac{-3}{3}=-1 \Rightarrow -45º\\&\\&(*)=\frac{(\sqrt 2)_{45º}}{(3 \sqrt 2)_{-45º}}=\Big( \frac{1}{3} \Big)_{45º-(-45º)}=\Big( \frac{1}{3} \Big)_{90º}\\&\\&de \ lo\ que \ se \ deduce:\\&\frac{C-A}{D-A}=\Big( \frac{1}{3} \Big)_{90º} \Rightarrow C-A=\Big( \frac{1}{3} \Big)_{90º}·(D-A) \Rightarrow\\&\\&\vec{AC}=\Big( \frac{1}{3} \Big)_{90º} \vec {AD}\\&\\&\Rightarrow giro \ 90º \ en A \Rightarrow ACD  \ es \ un \ triángulo \ rectángulo \ A=90º\\&\\&\frac{C-B}{D-B}=\frac{2i-(-1-i)}{2-2i-(-1-i)}=\frac{1+3i}{3-i}=(**)\\&\\&|1+3i|= \sqrt {1^2+3^2}=\sqrt{10}\\&\\&\alpha=arctan (3)\\&\\&|3-i|=\sqrt {3^2+1}=\sqrt {10}\\&\beta= arc tan \Big(\frac{-1}{3} \Big)\\&\\&(**)=\frac{(\sqrt {10})_{arctan3}}{(\sqrt {10})_{arctan (\frac{-1}{3})}}=1_{90º} \Longrightarrow\\&\\&\frac{C-B}{D-B}=1_{90º}  \Longrightarrow \vec{BC}=1_{90º} ·\vec{BD} \Rightarrow\\&\\&BCD \ es \ triángulo \ rectángulo \ con \ B=90º\\&\\&\end{align}$$

2)

En los dos triángulos ectángulos BCD y ACD, CD es la hipotenusa, luego CD es un diámetro y el centro es el punto medio de CD:

$$\begin{align}&M=\frac{C+D}{2}=(1,0)\\&\\&radio\\&r=| \vec{MC}|=|(1,2)|=\sqrt {1^2+2^2}=\sqrt 5\\&\\&ecuación \ circunferencia:\\&(x-1)^2+y^2=5\\&\\&Comprovamos \\&A=(-1,1) \Rightarrow(-2)^2+1^2=5\\&\\&B=(-1,-1) \Rightarrow (-1-1)^2+(-1)^2=5\\&\\&igualmente \ C  \ y \ D\end{align}$$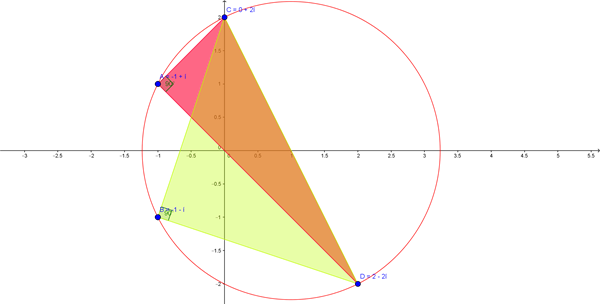

Saludos

;)

;)

;)

Recuerda que en una circunferencia el ángulo inscrito que abarca un diámetro es de 90º.

Luego CD es el diámetro

Bonito problema

Saludos

;)

;)