Cómo calcular la superficie de un Pentágono irregular?
Me gustaría saber cuál es la superficie de un Pentágono irregular, los 5 lados son distintos, ( 17,9 x 20'5 x 9,7 x 12 x 31,65). Lo he intentado dividiéndolo en 2 rectángulos y 2 triángulos y me sale 524. Agradecería mucho que alguien me lo confirmase o me diese su respuesta.
2 Respuestas

Espero que alguno de estos métodos te ayude:
http://www.universoformulas.com/matematicas/geometria/area-pentagono-irregular/
Sin el diseño desconozco las alturas de los triángulos, ya que, salvo que sea un triángulo, ninguna figura irregular tiene una disposición de ángulos fija.
Muchas gracias Josué, en mi Foto de perfil está el dibujo de dicho Pentágono, no sé cómo se pueden adJuntar fotografías en esta página web de otra forma.. Espero puedas contestarme y confirmar o corregir mi reSultado. Muchas gracias de antemano

Al escribir respuesta puedes pulsar en el primer icono de la barra que te aparece en el cuadro de escribir. No puedo ver la foto en grande y veo que hay medidas en una esquina, que no consigo leer. No quisiera darte un resultado erróneo.

Con las medidas que nos has facilitado, y usando al menos un ángulo recto, el pentágono que me sale es así, que dista un poco del que tú has dibujado. ¿Estás seguro de que está bien medido? Si las medidas son buenas, el dibujo no lo es. Si el área se parece a este pentágono, te calculo el área con esto.
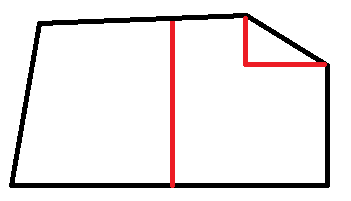
Muchas gracias! Madre mía me dejáis alucinando con vuestro control, dominio e interés por las matemáticas.. este Pentágono corresponde al terreno de mi casa y estaba interesado en saber los metros cuadrados que había aproximadamente...las mediciones las hice yo, y son muy aproximadas pero no exactas al milímetro. De ahí que quizás no os salgan las cUentas exactas y barajéis varias opciones.. muchas gracias a todos por el interés.

No hay de qué. Si aún necesitas el cálculo, basta con que tomes mediciones exactas =)
- Compartir respuesta

·
·
¡Hola Pablo!
Tienes que mandar el dibujo. Un pentágono irregular puede deformarse de forma que el área pueda valer desde 0 hasta los 524 que dices o incluso más. El método dependerá de la figura, puede ser triangulación o puede ser algún método especial si conocemos las coordenadas de los puntos.
Saludos.
·
·
LA foto de dicho Pentágono está en mi foto de perFil, ya que no sé cómo se pueden adjuntar fotografías en esta página web. Espero puedan Confirmar mi resultado o corregirme. Muchas gracias de ante mano
·
·
Las medidas no son compatibles. Dices que la altura es 16.4, pero si sumamos por otro lado 12 + 5.15 = 17.15
Entonces o están mal esas medidas o el lado de arriba y el de abajo no son paralelos. Y en eso caso habría que saber justo el ligar donde mide 16.4
Y la bases tampoco parecen bien dibujadas, arriba la longitud total sería
20.5 +8.20 = 28.70
Y eso en el dibujo es más largo que la base de abajo que mide 31.65, debería ser al revés.
En estos casos en los ejercicios pueden darte dibujos desfigurados, pero donde hay lados paralelos o perpendiculares no te mienten.
Repasa el dibujo y mira a ver si puedes corregirlo.
Saludos.
:
:
Si yo considero que los ladosde 20,5 y 31.65 son paralelos y que el de 31.65 y 12 son perpendiculares y desecho la medida de 16,4 el área se calcula como la de un trapecio quitando un triángulo.
Base mayor: 31.65
Base menor: 20.50 + 8.20 = 28.70
Altura 12+5.15 = 17.15
Area trapecio = (31.65+28.70)·17.15 / 2 = 517.50125
Y el triángulo que hay que quitar tiene por área
Area triángulo = 5.15 · 8.20 / 2 = 21.115
Con lo cual el area del pentagono sería:
517.50125 - 21.115 = 496.38625
Pero ya te digo que lo he hecho con unas suposiciones propias porque las medidas son incompatibles, lo primero que deberías hacer es asegurarte que las escribiste bien. Y si las escribiste bien deberías decir cuáles son las reales de verdad y aclarar si es vierdad lo de los lados paralelos y perpendiculares.
Y eso es todo, saludos.
:
:
¡Ah por cierto! Para poner imágenes aquí usa el icono de más a la izquierda, el que parece un paisaje de montañas. Puedes elegir entre subir una imagen que tengas en tu disco o dar la dirección de una imagen de internet.
La otra posibilidad es que la medida de 16.4 sea verdadera y tu hayas puesto las medidas 5.15 y 8.20. Y todo ello suponiendo ciertos los paralelismos y perpendicularidad del dibujo. Entonces esas medidas estarían mal.
La altura de ese triangulo de la esquina sería
16.4 - 12 = 4.4
Y la base sería
raíz(9.7^2 - 4.4^2) = 8.64465
Con esto la base menor del trapecio mediría:
Base menor = 20.5 + 8.64465 = 29.14465
Base mayor = 31.65
Altura = 16.4
Area trapecio = (29.14465 + 31.65)·16.4 / 2 = 498.51613
Y el área de la esquina que hay que quitar
4.4 · 8.64465 / 2 = 19.01823
Y el área del pentágono sería
498.51613 - 19.01823 = 479.4979
Y eso es todo.
Saludos.
:
:
Además tiene razón Josué. Si el ángulo es recto entonces las bases no son paralelas y si las bases son paralelas el ángulo no será recto. Tienes que asegurarte de las medidas y pon solamente las que te den, si tú has deducido alguna quítala. Y sobre todo aseguranos el tema de los paralelismos y ángulos rectos si son verdaderos o no.
Este sería el dibujo real. Como ves no sale bien del todo la medida del lado de 9.70 ya que las tres medidas no están bien sincronizadas hay que tomar dos como buenas y la otra sale de ello, yo tome como buenos los catetos y salió mal la hipotenusa.
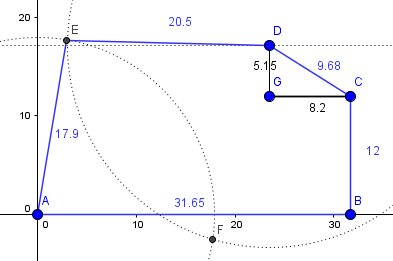
¡Gracias! Madre mía me dejáis alucinando con vuestro control, dominio e interés por las matemáticas.. este Pentágono corresponde al terreno de mi casa y estaba interesado en saber los metros cuadrados que había aproximadamente...las mediciones las hice yo, y son muy aproximadas pero no exactas al milímetro. De ahí que quizás no os salgan las cUentas exactas y barajéis varias opciones.. muchas gracias a todos por el interés.
¡Ah! Ahora le encuentro explicación a todo. Yo pensaba que era un ejercicio de colegio de los que ponen una figura distinta para dificultar la resolución.
Para hacerlo exacto primero hay que suponer que lo 5 lados son líneas rectas. Una vez supuesto eso nos tendrías que dar los 5 lados, tal como has hecho y luego las longitudes de dos diagonales desde un punto, por ejemplo AD y BD.
Mientras tanto, si la figura es como supuse en la primera respuesta sería un poco más de 496 pero no más de 500 creo yo. Pero lo mejor es que nos des esas dos diagonales que te decía con lo cual se puede dividir en tres triángulos y con teoremas de senos o productos vectoriales se puede calcular el área de cada uno.
- Compartir respuesta
Es gracioso tu lema de tu perfil. Es cierto que nada te impide ser el segundo o tercero en responder. Siempre y cuando aportes información nueva y no copies lo que otro ha dicho, como acabas de hacer. - Anónimo
Yo no sé de que selva vienes. Esto no es una carrera por contestar, se contesta bien y todo que se contesta es enriquecimiento para el usuario. Yo llevo aquí cinco años y nunca he tenido ningún problema con nadie, has tenido que venir tú a querer imponer tus normas. Mejor vete a contestar ginecología que de eso todos sabemos, pero algunos dejamos que sean los expertos de verdad los que contesten, sabelotodo. - Valero Angel Serrano Mercadal
Que te piensas, que me he copiado de tí como hallar áreas. Cuando hayas estudiado 5 años de matemáticas como yo y lleves otros cinco contestando preguntas aquí a diario de todas las clases, me toses. - Valero Angel Serrano Mercadal
Tampoco se tiene por que aportar imformación nueva. Una ecuación por ejemplo se resuleve de una forma determinada y no se le puede sacar nada nuevo, a ver si tú o yo vamos a tener el copyright de la fórmula por haber contestado el primero. - Valero Angel Serrano Mercadal
Y por supuesto que el perfil es curioso, tú me lo has sugerido con tu insolencia matinal. - Valero Angel Serrano Mercadal
Muchas gracias por las respuestas, el dibujo Del Pentágono está en mi foto de perfil ya que No sabia como adjuntar una imagen en esta página web. Espero puedan confirmar mi respuesta y/o corregirme. De todas formas mil gracias - Pablo Cacicedo
