Calcular el volumen del sólido al girar la región acotada

·

·

¡Hola José!

Haremos la representación gráfica de las funciones, pero la representación 2D que todavía estoy buscando el programa que represente funciones en 3D que me guste. Pondré solo una pequeña elipse para que se vea en torno de que eje gira.

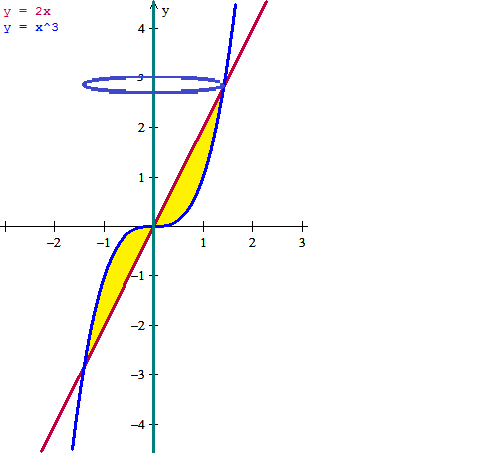
Como no nos acotan nada se supone que es el volumen de arriba y el de abajo. Y ambos seran iguales porque las dos funciones son simétricas respecto al punto (0,0) luego calcularemos la integral del volumen superior y multiplicaremos por 2.

El pequeño detalle que falta es que las funciones giran respecto al eje Y, entonces la fórmula exige que la función esté expresada como función de y, es decir, en vez de la función

y=f(x)

hay que usar

x = f^(-1)(y)

Las funciones serán

x=y/2

x= y^(1/3)

Y debemos saber los límites de integración en y

y/2 = y^(1/3)

y = 2 y^(1/3)

y^3 = 8y

los punto de intersección son

y=0

y^2 = 8

y = +- 2·sqrt(2)

Los que interesan a la parte superior son 0 y 2·sqrt(2)

Vamos ya con la integral

$$\begin{align}&V=\pi\int_{y_1}^{y_2}f(y)^2 dy\\&\\&\text{Si son dos funciones, al volumen exterior}\\&\text{hay que restar el interior}\\&\text{Y como calculamos solo el de arriba}\\&\text{multiplicaremos por 2}\\&\\&V=2\pi\int_0^{2 \sqrt 2}\left(\left(y^{\frac 13}\right)^2-\left(\frac y2  \right)^2\right)dy=\\&\\&2\pi\int_0^{2 \sqrt 2}\left(y^{\frac 23}-\frac {y^2}{4}\right)dy=\\&\\&2\pi \left[\frac 35 y^{\frac 53}-\frac{y^3}{12}  \right]_0^{2 \sqrt 2}=\\&\\&2\pi \left(\frac 35(2 \sqrt 2)^{\frac 53}-\frac{(2 \sqrt 2)^3}{12}  \right)=\\&\\&2\pi\left(\frac  35 (128 \sqrt 2)^{\frac 13}-\frac{16 \sqrt 2}{12}  \right)=\\&\\&2\pi\left(\frac 35·2^2·2^{1/3}·2^{1/6}-\frac 43 \sqrt 2  \right)=\\&\\&2\pi\left(\frac 35·4 \sqrt 2-\frac 43 \sqrt 2  \right)=\\&\\&2 \sqrt 2\pi \left(\frac {12}5-\frac 43  \right)=\\&\\&2 \sqrt 2\pi·\frac {16}{15}=\frac{32 \sqrt 2 \,\pi}{15}\\&\end{align}$$

Ha costado la parte final, a lo mejor podría haberlo hecho más corto calculando de otra forma.

Y eso es todo, saludos.

:

: