·
·
¡Hola Gabriella!
La función es un polinomio, por lo tanto continua, derivable y todo lo buena que se puede ser.
Si tiene máximos o mínimos relativos será en los puntos donde la derivada primera sea 0.
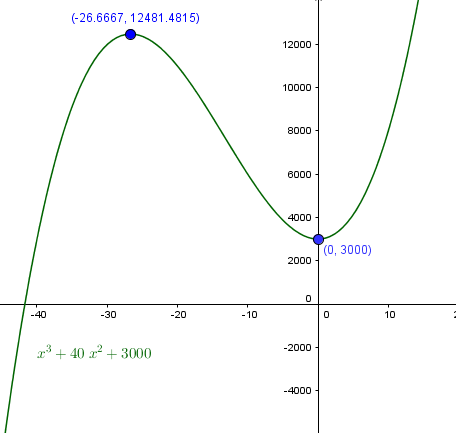
C(x) = x^3 + 40x^2 + 3000
derivcamos e igualamos a 0
C'(x) = 3x^2 + 80x = 0
x(3x + 80) = 0
x=0
3x + 80 =0
3x = -80
x = -80/3
Luego tenemos dos puntos críticos
x=0, x=-80/3
Calculamos la derivada segnda para saber la naturaleza de los puntos críticos
C''(x) = 6x + 80
C''(0) = 80 >0 luego en x = 0 hay un mínimo relativo
C''(-80/3) = 6(-80/3)+80 = -160 + 80 = -80 <0 luego hay un máximo
Luego el mínimo relativo es:
(0, 3000)
y el máximo relativo es
$$\begin{align}&\left(-\frac {80}3,\quad \left(-\frac{80}3\right)^3 + 40 \left(\frac{80}3\right)^2 + 3000\right)=\\&\\&\left(-\frac {80}3,\quad -\frac{512000}{27} + \frac{256000}9 + 3000\right)=\\&\\&\left(-\frac {80}3,\quad \frac{-512000+768000+81000}{27}\right)=\\&\\&\left(-\frac{80}{3},\frac {337000}{27}\right)\approx(-26.\overline 6,\;12481.48148)\\&\\&\end{align}$$Y esta es la gráfica que demuestra que están bien calculados.
:
:

