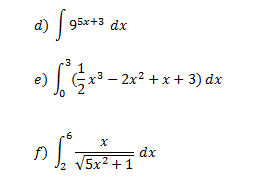;
d)
$$\begin{align}&\int 9^{5x+3} dx=\\&\\&5x+3=t\\&5dx=dt\\&dx=\frac{dt}{5}\\&\\&=\frac{1}{5} \int 9^t dt= \frac{1}{5} \frac{9^t}{ln9}=\frac{9^{5x+3}}{5 ln9}+C\\&\\&e)\\&\int_0^3(\frac{1}{2}x^3-2x^2+x+3)dx= \Bigg [\frac{x^4}{8}-\frac{2x^3}{3}+\frac{x^2}{2}+3x \Bigg]_0^3=\frac{45}{8}\\&\\&f)\\&5x^2+1=t\\&10dx=dt\\&x=2 \Rightarrow t=21\\&x= 6 \Rightarrow t=181\\&\\&\int _{21}^{181} t^{\frac{-1}{2}}·\frac{dt}{10}=\frac{1}{10} \Bigg [2t^{\frac{1}{2}} \Bigg]_{21}^{181}=\frac{2}{10} \Big( \sqrt{181} -\sqrt {21})=\\&\\&=\frac{1}{5} \Big( \sqrt{181} -\sqrt {21})=1.77420967\end{align}$$Saludos
;)
;)