Tasa de cambio y criterio de la primera derivada Su función de ingresos es la siguiente:
Su función de ingresos es la siguiente:
I(q)=5q^3+2q^2-3q+25
A partir de dicha función, se pide determinar lo siguiente:
- Determinar valores máximos y mínimos de la función.
- Determinar puntos de inflexión.
- Determinar intervalos de crecimiento y decrecimiento.
- Determinar intervalos de concavidad.
Respuesta de Valero Angel Serrano Mercadal
1
·
·
¡Hola Amee!
$$\begin{align}&1)\quad I(q) = 5q^3+2q^2-3q+25\\&\\&\text{derivamos e igualamos a 0}\\&\\&I'(q) = 15q^2+4q-3=0\\&\\&q=\frac{-4\pm \sqrt{16+180}}{30}=\\&\\&\frac{-4\pm 14}{30}= -\frac 35 \;y\;\frac{1}{3}\\&\\&\text{La derivada segunda es}\\&\\&I''(q) = 30 q +4\\&\\&I''\left(-\frac 35\right)=-\frac{90}{5}+4=-14\lt 0\implies máximo\\&\\&I''\left( \frac 13\right)=10+4 = 14 \gt 0 \implies mínimo\\&\\&\text{El máximo es}\\&\\&I\left(-\frac 35\right)=I(-0.6)=5·(-0.6)^3+2·(-0.6)^2-3(-0.6)+25=26.44\\&\\&\text{Luego es el punto } (-0.6,\;26.44)\\&\\&\text{El mínimo es}\\&\\&I\left(\frac 13\right)=\frac 5{27}+\frac 29-1+25 = 24.40740741\\&\\&\text{Luego es el punto }\left(0.33\overline 3,\;24.\overline{4074}\right)\\&\\&\\&2)\text{ Puntos de inflexión donde la derivada segunda es 0}\\&\\&I''(q)= 30q+4=0\\&\\&q= -\frac{4}{30}=-\frac 2{15}=0.133\overline 3\\&\\&\text{Y el punto es:}\\&\\&I(-0.133\overline 3)=5·(-0.1\overline 3)^3+2(-0.1\overline 3)^2-3·(-0.1\overline 3)+25=25.4237037\\&\\&\text{El punto de inflexión es: } \left(-0.1\overline 3,\;25.4237037 \right)\\&\\&\\&3)\\&\text{Crecimiento antes de máximo y después de mínimo}\\&(-\infty, -0.6) \cup(0.\overline 3,\infty)\\&\\&\text{decrecimiento antes de mínimo y después de máximo}\\&(-0.6,\;0.\overline 3)\\&\\&\text{recuerda que la barrita de arriba es que se repite el ciclo}\\&\\&\\&\text{4) Concavidad hacia arriba si derivada segunda positiva}\\&\text{y hacia abjo si es negativa}\\&\\&\text{Tomemos } (-1)\implies I''(-1) =30(-1)+4=-26\\&\text{Tomemos } (0)\implies I''(0)=4\\&\\&(-\infty,-0.1\overline 3) \text{ Cóncava hacia abajo}\\&\\&(-0.1\overline 3,\;\infty) \text{ Cóncava hacia arriba}\end{align}$$Y esta es la gráfica para comprobar que esta bien. Fíjate la gran depsroporción que hay en los ejes, pero es la forma en que se ve bien.
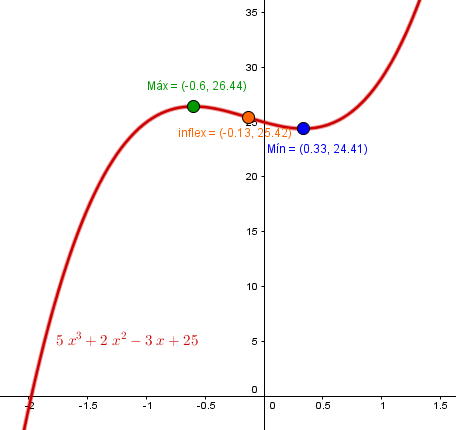
Y eso es tod, espero que te sirva y lo hayas entendido. Si no es así, pregúntame. Y si ya está bien, no olvides valorar la respuesta.
Saludos.
:
:
