Análisis marginal.A partir de la función anterior, se pide:a) Calcular la derivada completamente simplificada.
A partir de la función
f(x)=(2x-1)^2 (9-x)
Calcular la derivada completamente simplificada.
b) Determinar los valores críticos.
c) Concluir si los valores críticos son máximos o mínimos.
d) Determinar intervalos de crecimiento y decrecimiento.
1 respuesta
·
·
¡Hola Amee!
Lo de lo más simplificada posible a lo mejor no te gusta. Yo la voy a hacer lo más simplificada posible para calcular fácilmente las raíces, porque eso es lo que me van a pedir después. Si la primera derivada no hiciera falta para nada y lo que fuera importante fuera la segunda, entonces la primera la simplificaría de otra forma.
$$\begin{align}&f(x)=(2x-1)^2(9-x)\\&\\&f'(x) = 2(2x-1)·2·(9-x)+(2x-1)^2(-1) =\\&\\&(2x-1)(36-4x-2x +1) = (2x-1)(37-6x)\\&\\&\text{esa es la simplificación mejor para lo que viene}\\&\\&\\&\\&\text{2) Los valores críticos son los que }f'(x)=0\\&\\&(2x-1)(37-6x)=0\\&2x-1=0 \implies 2x=1 \implies x=\frac 12\\&37-6x=0\implies6x=37\implies x=\frac{37}{6}\\&\\&\text{3) La derivada segunda es}\\&f''(x)=2(37-6x)+(2x-1)·(-6)=\\&2(37-6x-6x+3)=2(40-12x)\\&\\&f''\left(\frac 12\right)=2(40-6)=72\implies mínimo\\&\\&f''\left( \frac {37}6\right)=2(40-74)=-68\implies máximo\\&\\&\text{4) Antes de un mínimo decrece, luego crece}\\&\text{Antes de un máximo crece y luego decrece, luego}\\&\\&\left(-\infty,\frac 12\right) decreciente\\&\\&\left( \frac 12,\frac{37}{6}\right) creciente\\&\\&\left( \frac{37}{6},\infty\right) decreciente\end{align}$$Esta es la gráfica que confirma los resultados:
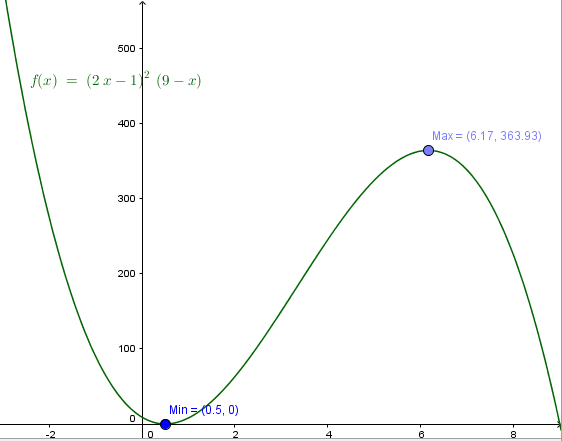
Y eso es todo. Espero que te sirva y lo hayas entendido. No olvides valorar las respuestas para poder seguir recibiendo más.
Saludos.
:
:
