Segunda parte de las integrales impropias.
Para cumplir con las reglas, subo la segunda integral impropia en otra pregunta.
Calcular las siguientes integrales impropias:
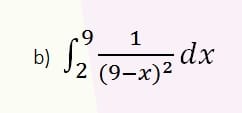
2 Respuestas
Respuesta de Lucas m
1
;)
Hola jose!
$$\begin{align}& \int \frac{1}{(9-x)^2} dx= - \frac{(9-x)^{-2+1}}{-1}=(9-x)^{-1}=\frac{1}{9-x}\\&\\&\int_2^9 \frac{1}{(9-x)^2} dx= \frac{1}{9-x} \Bigg |_2^9=\lim_{x \to 9} \frac{1}{9-x}-\frac{1}{7}=\frac{1}{0}-\frac{1}{7}=\infty\end{align}$$saludos
;)
;)
Respuesta de Valero Angel Serrano Mercadal
1
·
·
¡Hola José!
Si lo fuéramos a hacer muy estricto conforme a la definición sería:
$$\begin{align}&\int_2^9 \frac{1}{(9-x)^2}dx = \lim_{k\to 9^-}\int_2^k \frac{1}{(9-x)^2}dx=\\&\\&\lim_{k\to 9^-}\frac{1}{9-x}\Bigg|_2^k=\lim_{k\to9^-}\left(\frac{1}{9-k}-\frac{1}{9-2}\right)=\\&\\&+\infty-\frac 17 = +\infty\end{align}$$Luego la integral es divergente.
Y eso es todo, saludos.
:
: