Calcular la siguiente integral por medio de sustitución trigonométrica
Espero me puedan ayudar con esta integral.
Calcular la siguiente integral por medio de sustitución trigonométrica:
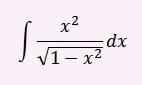
1 Respuesta
Respuesta de Valero Angel Serrano Mercadal
1
·
·
¡Hola Jose!
Esta es dentro de las sustitución trigonométrica la ue menos me disgusta.
Esta claso que x debe set sent (o cost da lo mismo)
$$\begin{align}&\int \frac{x^2}{\sqrt{1-x^2}}dx=\\&\\&x=sent\\&dx=cost \;dt\\&\\&\int \frac{sen^2t}{\sqrt{1-sen^2t}}·cost\; dt=\\&\\&\int \frac{sen^2t}{cost}· cost \;dt=\\&\\&\int sen^2t\;dt=\\&\\&\int \left(\frac{1}{2}-\frac{\cos 2t}{2}\right)dt=\\&\\&\frac t2-\frac {sen \,2t}4+C\\&\\&\frac 12arcsen\,x-\frac{2sent·cost}{4}+C=\\&\\&\frac 12arcsen\,x-\frac{x·\sqrt{1-x^2}}{2}+C=\\&\\&\frac {arcsen \,x - x \sqrt{1-x^2}}{2}+C\end{align}$$:
:
