Me piden encontrar los extremos relativos, los puntos de inflexión y gráfica la siguiente función.
Me piden encotra los extremos relativos, los puntos de inflexión y gráfica la siguiente función. Pero no comprendo si primero debo resolver lo que me pide la función, ya que son cosas diferentes
$$\begin{align}&Con la función f(x) = x³ - 6x² + 15, demostrar que existe c∈[-3,0] tal que f(c)=0\end{align}$$
1 Respuesta
·
·
¡Hola Ana Belén!
Eso deberías saberlo tú. Como no es muy larga haré las dos cosas.
El teorema de Bolzano dice que si una función es continua en [a, b] y toma valores con signo contrario en a y b entonces existe un valor c en (a,b) tal que f(c)=0
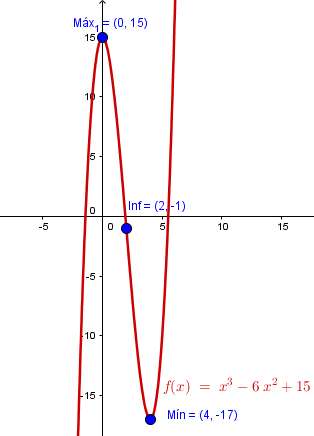
La función
f(x) = x^3 - 6x^2 + 15
es continua en todo R, luego lo es en [-3, 0]
f(-3)=-27-54+ 15 = -66
f(0) = 15
Toma signos contrarios, luego existe c en (-3,0) tal que f(c)=0
Y si existe en (-3,0) existe en [3,0]
------------
Los extremos relativos de una función derivable tienen derivada 0
f'(x) = 3x^2-12x = 0
3x(x-4)=0
son
x=0, x=4
Veamos si son máximos o mínimos, para ello usamos el criterio de la derivada segunda.
f''(x) = 6x-12
f''(0) = -12 <0 luego es máximo
f''(4) = 24-12= 12 >0 luego es mínimo
El máximo relativo es (0,f(0)) = (0, 15)
El mínimo relativo es (4,f(4)) = (4, 64-96+15) = (4, -17)
Los puntos de inflexión tienen derivada segunda cero y tercera sistinta de 0
6x-12=0
6x=12
x=2
la tercera es
f'''(x)=6
Luego es punto de inflexión, y es
(2,f(2)) = (2, 8 -24+15) = (2,-1)
Y con estas cosas y algunos puntos o con algunas cosas más como saber que el límite en -infinito es - infinito y en +infinito es + infinito, o que en el intervalo (-infinito, 2) es cóncava hacia abajo y en (2,+infinito) es cóncava hacia arriba, se hace la gráfica.
Y eso es todo, saludos.
:
:
