Entre que contestas o no lo voy haciendo. Lo de calcularlo con las reglas es muy sencillo
$$\begin{align}&\lim_{x\to 3} \frac{x-2}{2x}= \frac{3-2}{6}=\frac 16\\&\\&\text{Demostrarlo por definición significa encontrar un }\delta\gt 0\\&\text{para cualquier }\epsilon \gt 0\text{ que nos den. De tal forma}\\&\text{que si x cumple }0\lt|x-3|\lt \delta\text{, entoces se cumple}\\&\\&\bigg|\frac{x-2}{2x}-\frac 16\bigg|\lt\epsilon\\&\\&\text{para poder calcularlo primero ponemos esto último}\\&\text{en función de |x-3|}\\&\\&\bigg|\frac{x-2}{2x}-\frac 16\bigg|=\bigg|\frac{3x-6-x}{6x}\bigg|=\bigg|\frac{2x-6}{6x}\bigg|=\frac{|x-3|}{|2x|}\\&\\&\text{Tomaremos un }\delta \text{ primario de valor 1, con lo cual será}\\&\\&0\lt |x-3|\lt 1\\&-1\lt x-3\lt 1\\&2 \lt x\lt 4\\&\\&\text{Demos calcular el máximo de }\frac{|x-3|}{|2x|}\text{ en (2, 4)}\\&\text{lo cual es el máximo de } \frac{3-x}{2x} \;en\; (2,3) \text{ y de } \frac{x-3}{2x}\;en\;(3,4)\\&\\&\frac 3{2x}-\frac 12 \text{ es decreciente, luego el máximo en 2. }Máx_1=\frac 14\\&\\&\frac 12-\frac{3}{2x}\text{es creciente, luego el maxímo en 4. }Máx_2=\frac 18\\&\\&\text{Luego el máximo es }\frac 14\\&\\&\text{Esto significa que si }\epsilon \gt \frac 14\text{ tomaremos }\delta=1\\&\\&\text{Y ahora buscaremos el }\delta \text{ para un }\epsilon\text{ menor}\\&\text{que eso es lo que verdaderamente importa}\\&\\&\text{Si tomamos un }\delta \lt1 \text{ ya vimos que }\\&x\in(2,4)\implies 2x\in(4,8)\implies |2x|\in (4,8)\\&\text{El denominador que más grande puede hacer }\frac{|x-3|}{|2x|}\\&\text{el menor, ya que al dividir por menos toca más, luego}\\&\frac{|x-3|}{|2x|}\le \frac{|x-3|}{4}\\&\\&\text{Resumiendo, si }\epsilon\le \frac 14 \;\text{ tomaremos }\delta \le 1\\&\text{y nos aseguramos que si}\\&0\lt|x-3|\lt \delta\implies \bigg|\frac{x-2}{2x}-\frac 16\bigg|\le \frac{|x-3|}{4}\lt \frac{\delta}{4}\\&\\&\text{luego tomando }\delta =4 \epsilon \text{ tendremos }\bigg|\frac{x-2}{2x}-\frac 16\bigg|\lt \frac{4\epsilon}{4}= \epsilon\\&\\&\text{y por lo tanto se cumple la definición de límite cuando }\epsilon\le \frac 14\\&\\&\text{Y finalmente unificamos la elección de }\delta \text{ para los dos casos,}\\&\text{cuando }\epsilon \gt \frac 14 \text{o cuando }\epsilon\le \frac 14\\&\\&\delta=mín\{1,\;4\epsilon\} \\&\\&\\&\\&\\&\\&\end{align}$$Y ese es el delta. Esa elección indica que en las inmediaciones de x=3 la pendiente es menor de 1/4 = 0.25
Como efectivamente atestigua la gráfica que indica una pendiente de 0.11
O como indicaría si calcularamos la derivada que no viene al caso.
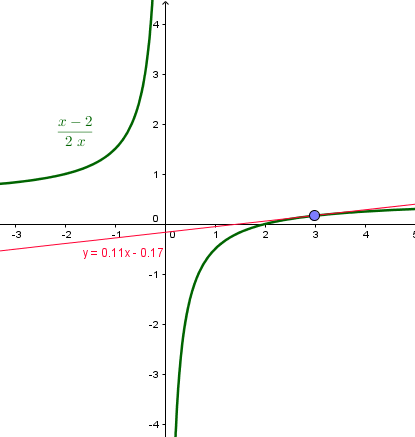
:
:


