Calcular las alturas del cono y cilindro para área superficie mínima

;)
Hola Jhon!

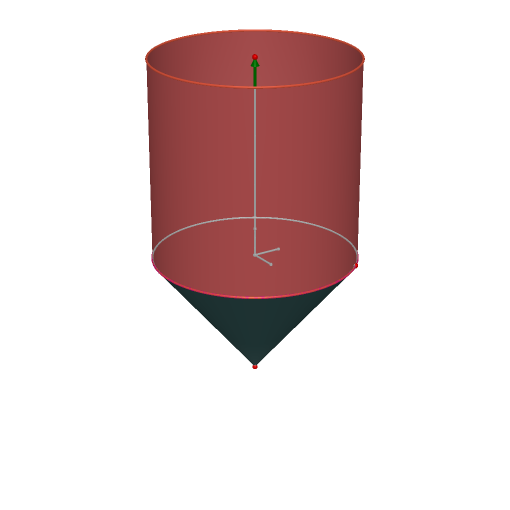
r=2 pies

V=100 pies^3

Sea h la altura del cono. Sea g su generatriz

Sea y la altura del cilindro

El área a optimizar es la suma del área lateral del cono (pi·r·g) más el área lateral del cilindro (2·pi·r·y) más el área superior (pi·r^2)

$$\begin{align}&100=\frac{1}{3} \pi r^2h+ \pi  r^2y\\&\\&100=\frac{1}{3} \pi 4h+ 4 \pi y\\&\\&4 \pi y=100- \frac{4 \pi}{3}h\\&\\&y=\frac{25}{\pi}- \frac{h}{3}\\&\\&A= \pi r g+2 \pi r y+ \pi r^2\\&A= \pi r \sqrt {r^2+h^2}+2 \pi r y+\pi r^2\\&\\&A(h)=2 \pi \sqrt {4+h^2}+4 \pi(\frac{25}{\pi}- \frac{h}{3})+4 \pi\\&\\&A(h)=2 \pi \sqrt {4+h^2}+100-\frac{4 \pi}{3} h+ 4 \pi\\&Derivando:\\&A'(h)= 2 \pi \frac{1}{2 \sqrt {4+h^2}}(2h)- \frac{4 \pi}{3}\\&\\&A'(h)=  \frac{2 \pi h}{\sqrt {4+h^2}}- \frac{4 \pi}{3}\\&A'=0\\& \frac{2 \pi h}{\sqrt {4+h^2}}- \frac{4 \pi}{3}=0\\&\\&  \frac{2 \pi h}{\sqrt {4+h^2}}= \frac{4 \pi}{3}\\&\\&3h=2 \sqrt{4+h^2}\\&elevando \ al \ cudrado:\\& 9h^2=4(4+h^2)\\&5h^2=16\\&h= \frac{4}{\sqrt 5}= \frac{4 \sqrt 5}{5}=1.7888 \ \ pies\\&Comprobación \ del \ mínimo \ :\\&A'(1)= \frac{2 \pi}{\sqrt 5}- \frac{ 4 \pi}{3}=-1.3<0 \rightarrow decreciente\\&A'(2)=\frac{4 \pi}{\sqrt 8}- \frac{ 4 \pi}{3}=0.25>0 \rightarrow creciente\\&luego \ 1,7888 \ es \ un \ mínimo\\&altura \ cilindro:\\&y=\frac{25}{\pi}- \frac{4 \sqrt 5}{15}=7.36 \ pies\\&\\&\\&\end{align}$$

recuerda  votar la respuesta

Saludos

;)

;)