Evalúa las siguientes integrales usando la segunda parte del teorema fundamental del cálculo
Pueden ayudarme con estas integrales usando la segunda parte del teorema fundamental del calculo. Gracias!
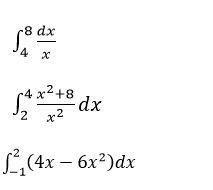
2 respuestas
Respuesta de Valero Angel Serrano Mercadal
2
·
·
¡Ho_la Luis!
Yo haré los que quedan.
$$\begin{align}&\int_2^4 \frac{x^2+8}{x^2}dx=\int_2^4\left( 1+\frac 8{x^2}\right)dx=\\&\\&\int_2^4(1+8x^{-2})dx =\left[x+8·\frac{x^{-1}}{-1} \right]_2^4=\\&\\&\left[x-\frac 8x \right]_2^4=4-2-2+4=4\\&\\&-----------------\\&\\&\int_{-1}^2(4x-6x^2)dx=\left[2x^2-2x^3 \right]_{-1}^2=\\&\\&8-16-2-2=-12\end{align}$$:
:
Respuesta de Lucas m
1
;)
Hola Luis!
$$\begin{align}&\int_4^8 \frac{dx}{x}= lnx \Bigg|_4^8=ln8-ln4=ln2^3-ln2^2=3ln2-2ln2=ln2=0.693147806····\end{align}$$