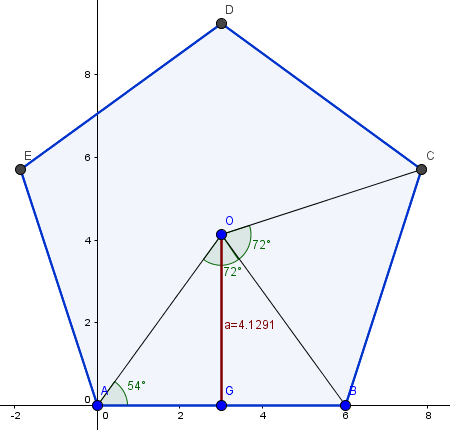
Calcula la área del pentágono
Dibuja un pentágono regular de 6 cm de lado. Determina la longitud del apotema.
2 respuestas
:)
Hola!
En el siguiente enlace: Cómo encontrar la superficie de un pentágono verás 3 formas de hallar la superficie de un pentágono regular en función de los datos que se te proporcionen.
Ahora bien: dado que en el ejercicio que planteas sólo se te brinda la longitud de sus lados, entonces la fórmula que deberías utilizar es:
Sup = (5 * L²) / [4 * tan(36º)]
Siendo "L" la longitud de los lados (L = 6 cm).
¡Gracias!
:)
Fue un gusto...
Y, por cierto: a mí puedes puntuarme "como te venga en gana" puesto que no te he ayudado para ser puntuado sino por solidaridad y ganas de ayudar, nomás.
¡Hasta la próxima!
:)
·
·
¡Hola Majo!
Este es el pentágono realizado con Geogebra. Luego te diré cómo calcule el apotema que fue necesario para calcular el centro y completar la gráfica.
Para calcular el apotema calculamos primero el ángulo central de uno de los triángulos que se forman. Como son 5 triángulos el ángulo de cada uno es
360º/5 = 72º
Ahora calculamos los otros ángulos del triángulo, como es isósceles son iguales, entonces miden
(180º-72º) / 2 = 108º/2 = 54º
Ahora tenemos un triángulo rectángulo AGO del que conocemos el cateo adyacente que mide la mitad del lado del hexágono
6cm/2 = 3cm
y conocemos él ángulo que es 54º.
La tangente de un ángulo se define como
tg(alfa) = (cateto opuesto) / (cateto adyacente)
luego
(cateto opuesto) = (cateto adyacente)·tg(alfa)
Ese cateto opuesto es el apotema, luego:
ap = 3·tg(54º) = 4.12914576 cm
:
.
¡Gracias!
Si no puntúas excelente esta pregunta ya no habrá más repuestas mías a tus preguntas.
Si acaso se me olvidó calcular el área, pero en en el enunciado solo preguntabas por el apotema, y hay muchos ususarios que ponen cualquier título que luego no tiene qie ver con el enunciado, lo que queda es una chorrada, aplicamos la fórmula del área de un polígono regular.
A = P·ap / 2 = 5 · 6 · 4.12914576/2 = 61.9371864 cm^2
Recuerda subir la nota aquí abajo.