¿Se puede resolver mediante integración por sustitución?
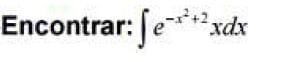
¿Se puede por el método de sustitución? ¿O es de las complicadas?
2 Respuestas
Respuesta de Lucas m
1
Respuesta de Valero Angel Serrano Mercadal
1
