Realizar los sigueinete ejercicios de derivadas calculo difeerncial
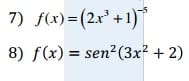
Buenas tardes amigos gfracia por su ayuda al igual que los anteriores por favor mencionar las propiedades que utilizaron para soluicnar gracias feliz rade
Respuesta de Valero Angel Serrano Mercadal
1
1 respuesta más de otro experto
Respuesta de Lucas m
1
