Las derivadas resolver ejercicios de calculo diferencial
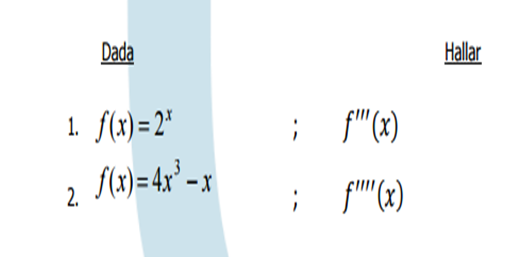
Calcula las siguientes derivadas de orden superior. Nnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnn
2 respuestas
Respuesta
3
Respuesta de Valero Angel Serrano Mercadal
1
