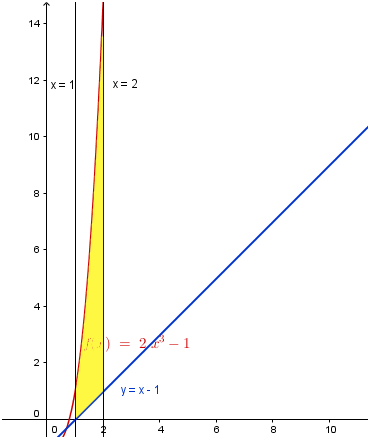
Hallar el área situada entre las curvas y=x-1 e y...

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...
2 Respuestas
Respuesta de Mario Rodríguez
Respuesta de Valero Angel Serrano Mercadal
2