Un ejercicio de calculo o matemáticas para un explicación muy excelente
Estos dos ejercicios son de derivadas de orden superior para una buena solución
1 respuesta
Respuesta de Valero Angel Serrano Mercadal
2
·
·
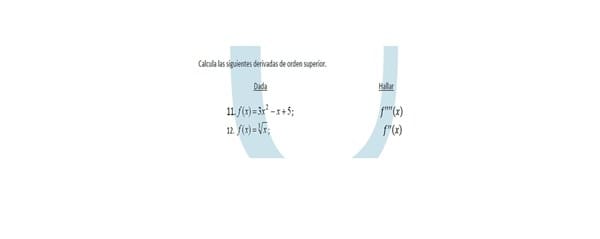
$$\begin{align}&\text{Usaremos estas reglas}\\&(f+g)'=f'+g'\\&(k·f)'=k·f'\qquad\text{Siendo k una constante de }\mathbb R\\&(x^n)'=nx^{n-1}\\&\text{Se puede deducir de la anterior, pero es mejor aplicar}\\&\text{directamente que la derivada de una constante es 0}\\&\\&11)\quad f(x)=3x^2-x-5\\&\\&f'(x)=6x-1\\&\\&f''(x)=6\\&\\&f'''(x)=0\\&\\&f''''(x)=0\\&\\&\\&12)\quad f(x) = \sqrt[3]x\\&\\&\text{Para trabajar bien lo ponemos en exponencial}\\&\\&f(x)=x^{\frac 13}\\&\\&f'(x) = \frac 13x^{\frac 13-1}=\frac 13 x^{-\frac 23}\\&\\&f''(x)= \frac 13·\left(-\frac 23 \right)x^{-\frac 23-1}=-\frac{2}{9}x^{-\frac 53}=-\frac{2}{9 \sqrt[3]{x^5}}\end{align}$$Y eso es todo, s a l u d o s!
:
:
