En las siguientes ecuaciones, determinar las coordenadas del vértice y del foco; el eje de simetría, la directriz de la parábola

·

·

¡Hola Diego!

Haré solo uno, en una sola pregunta no pueden ir dos ejercicios de cierta envergadura. Si quieres manda le otro en otra pregunta.

La ecuación canónica puede ser de dos tipos:

$$\begin{align}&\text{Parábolas verticales}\\&(x-h)^2=2p(y-k)\\&\\&\text{Parábolas horizontales}\\&(y-k)^2=2p(x-h)\\&\\&y^2-6y + 8x + 25=0\\&\text{Es la y la que lleva el cuadrado, luego horizontal}\\&\\&\text{Completo cuadrados}\\&(y-3)^2-9+8x+25=0\\&(y-3)^2=-8x-16\\&(y-3)^2= -8(x+2)\\&(y-3)^2 = 2·(-4)(x+2)\\&\\&\text{Ya está en forma canónica}\\&\\&\text{El vértice es }(-2,3)\\&\\&\text{Es horizontal, el eje de simetia es la horizontal}\\&\text{que pasa por el vértice}\\&y=3\\&\\&\text{El foco es el punto sobre el eje de simetría tal que}\\&\text{la distancia con signo del vértice a él es p/2, eso es:}\\&F_x-V_x= \frac p2\text{ no lo confundas con } V_x-F_x= \frac p2\\&\\&F_x-(-2)=-\frac 42\\&F_x+2 = -2\\&F_x=-4\\&Luego\\&F=(-4,3)\\&\\&\text{La directriz es la recta vertical  x=d  cuya distancia al}\\&\text{vertice es p/2.  Ojo es distancia con signo, esto significa}\\&V_x-d = \frac p2  \text{ no lo confundas con }\;d-V_x=\frac p2\\&\\&-2-d = -\frac 42\\&-2-d=-2\\&-d=0\\&d=0\\&\text{Luego la directriz es}\\&x=0\\&\end{align}$$

Conviene hacer una gráfica para ver que todo está bien, gracias a ella me di cuenta que había fallado en un signo.

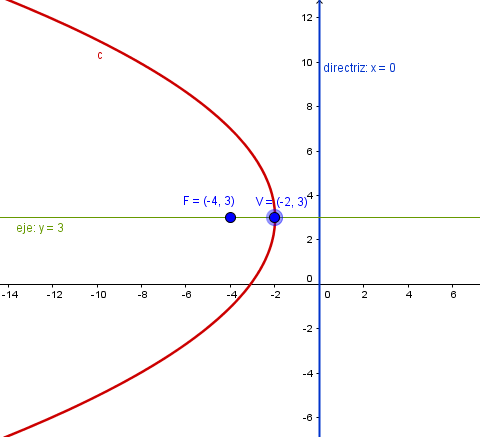
Y eso es todo, saludos.

:

: