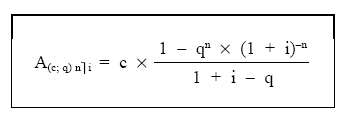Calcular el tiempo en el que se genera un monto

·

·

¡Hola José Luis!

Para esto hay que usar una fórmula que uno no se acuerda nunca, deja que la busque, es el valor de una renta con depósitos crecientes en progresión geométrica.

Yo no sé que notación usaréis, todas son distintas, aquí tienes por ejemplo la de mi libro de referencia

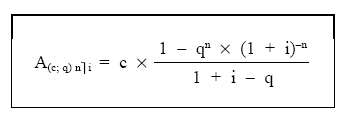
Que es el valor actual de una renta en progresión geométrica q de n cuotas de valor inicial c con interés períodico i.

Lo que pasa es que nosotros necesitamos el valor final, luego eso habra que multiplicarlo por (1+i)^n

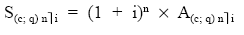
Yo no uso esas notaciones porque no sé si las usáis vosotros y porque son complicadas la verdad y se ven muy mal los subíndices.

Q es la razón de la progresión, si aumentan el 0.5% = 0.005 entonces

q=1.005

La tasa de interés que necesitamos es la efectiva mensual, como la que nos dan es la efectiva anual el calculo se realiza así

$$\begin{align}&i_m=(1+i_a)^{\frac 1{12}}-1=1.089^{\frac 1{12}}-1=\\&1.007130287-1 = 0.007130287\\&\\&\text{Y sustituyendo datos será}\\&S_{(700;\;1.05)n¬\,0.007130287)}=\\&\\&1.007130287^n·700·\frac{1-1.005^n(1.007130287)^{-n}}{1.007130287-1.005}\ge 20000\\&\\&1.007130287^n·\left( 1-\left(\frac{1.005}{1.007130287}\right)^n \right)\ge \frac{20000·0.002130287}{700}\\&\\&1.007130287^n-1.005^n\ge0.06086534286\end{align}$$

Y esto no se puede calcular se necesita ordenador, esta vez se lo dejaremos a la página WolframAlpha

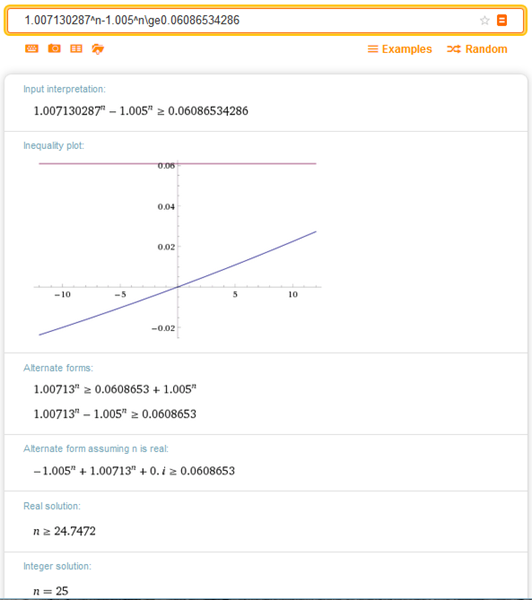
De donde son necesarios 25 meses.

Yo no sé como resolvéis esto, otra posibilidad es con una hoja de cálculo, como Excel por ejemplo, y quedaría así:

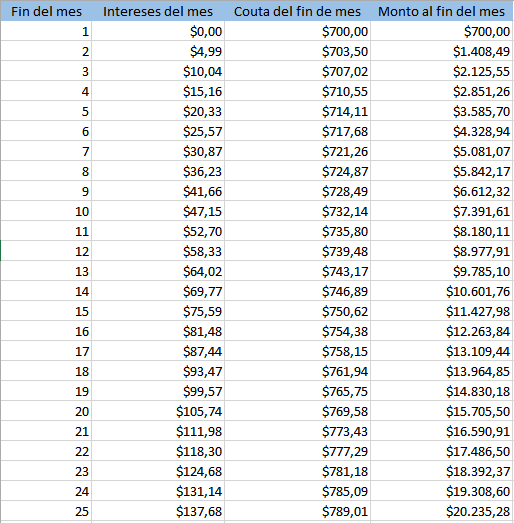
Lo cual confirma que los cálculos que hicimos están bien.

Te dejo la hoja por si quieres examinar las fórmulas y te puede servir para hacer ejercicios similares.

https://drive.google.com/file/d/0B3nG6r7qbZZ_bGJrMGFvcm1oVHM/view?usp=sharing 

Y eso es todo, espero que te sirva

Sa lu dos.

:

--