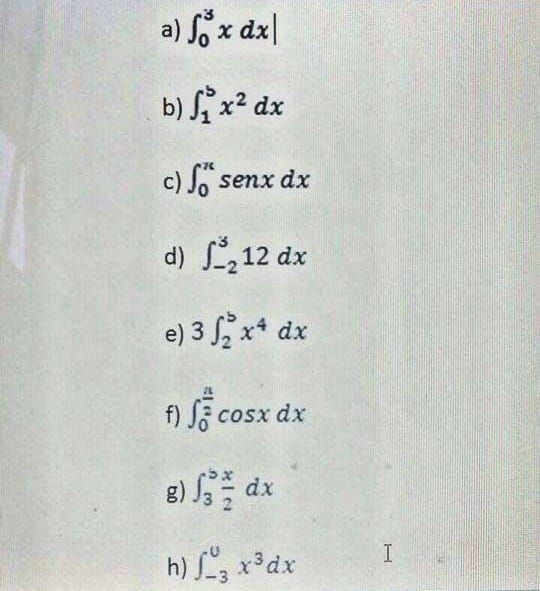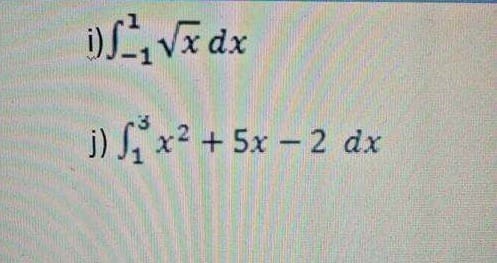Calculo diferencial e integral. La integral definida de una función 1. Realiza los siguientes ejercicios
A) ʃo3 x dx
B) ʃ1b x2 dx
C) Ʃon senx dx
D) ʃ3_2 12 dx
E) 3 ʃb2 x4 dx
F) ʃu_3 x3 dx
G) ʃ1_1 √x dx
H) ʃ31 x2 + 5x – 2 dx
2 Respuestas
Y si no puedes hacer eso escribe en cada integral lo que es la función, el límite inferior y el superior, porque en los que no ha hecho Lucas tengo muchas dudas sobre cuál es cuál, por una parte lo normal es que el inferior sea el primero, pero por otra parte también es normal que el inferior lleve delante _ y el superior lleve delante ^ con lo cual no me decido por nada porque veo contradicciones.
Sa lu dos.
:
:
Le envió las imágenes, espero que así estén claras, y disculpe no revise que estaban mal los enunciados
Aunque son fáciles son demasiados ejercicios para una pregunta, en integrales fáciles estamos contestando dos ejercicios como mucho por pregunta, haré unos cuantos pero no todos. Los que falten los puedes mandar en otra pregunta.
$$\begin{align}&c) \int_0^\pi senx\;dx=-\cos x\bigg|_0^\pi=-(-1)+1=2\\&\\&d) \int_{-2}^3 12\,dx=12x\bigg|_{-2}^3=36+24=60\\&\\&e) \quad3\int_2^bx^4dx= 3·\frac{x^5}{5}\bigg|_2^b=3\left(\frac{b^5}{5}-\frac {32}5 \right)=\frac{3b^5-96}{5}\\&\\&f) \int_0^{\frac \pi 2}cosx \;dx= sen\,x\bigg|_0^{\frac \pi 2}=1-0=1\\&\\&g) \int_3^b \frac x2dx= \frac {x^2}{4}\bigg|_3^b= \frac{b^2-9}{4}\\&\\&h) \int_{-3}^u x^3 dx = \frac{x^4}{4}\bigg|_{-3}^U = \frac{U^4-81}{4}\end{align}$$Y eso es todo, saludos.
:
:
;)
Entiendo esto en los dos primeros:
$$\begin{align}&A)\\&\int_o^3xdx= \frac{x^2}{2} \Bigg |_0^3=\frac{9}{2}\\&\\&B)\\&\int_1^b x^2dx= \frac{x^3}{3} \Bigg|_1^b=\frac{b^3}{3}-\frac{1}{3}\\&\\&E)\\&3 \int_b^2 x^4dx= 3 \frac{x^5}{5} \Bigg |_b^2= \frac{3}{5} ( 32-b^5 )\end{align}$$saludos
;)
;)