Sacar el límite por Ley de L. Hospital a estos límites:
¿Cómo puedo sacar el límite a estos límites por esta ley?
Hay algunos límites que no me dan, me dan n/0 siendo n número natural al hacer este procedimiento.
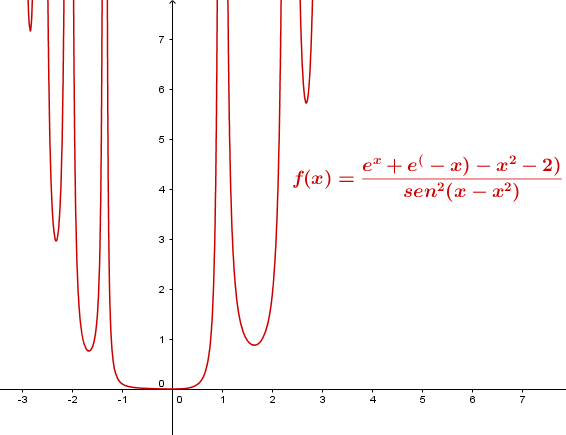
$$\begin{align}&\lim_{x \to 1} \frac{ln(2x^2-1)}{Tan (x-1)}\end{align}$$$$\begin{align}&\lim_{x \to 0} \frac{e^x+e^{-x}-x^2-2}{sen^{2} (x-x^2)}\end{align}$$
1 Respuesta
Respuesta de Valero Angel Serrano Mercadal
1
·
·
¡Hola Carlos!
Si dan n/0 entonces el límite es infnito.
$$\begin{align}&L=\lim_{x\to 1} \frac{ln(2x^2-1)}{tan(x-1) }=\frac{ln \,1}{tg\,0}= \frac 00\\&\\&\text{Derivamos numerador y denominador}\\&\\&L= \lim_{x\to 1} \frac{\frac {4x}{2x^2-1}}{sec^2(x-1)}=\frac{\frac{4}{1}}{sec^2(0)}=\frac 41=4\\&\\&------------------\\&\\&\text{Y el segundo}\\&\\&L=\lim_{x\to 0}\frac{e^x+e^{-x}-x^2-2}{sen^2(x-x^2)}=\frac{1+1-0-2}{sen^2 0}= \frac 00\\&\\&\text{derivamos numerador y denominador}\\&\\&L=\lim_{x\to 0} \frac{e^x-e^{-x}-2x}{2sen(x-x^2)·\cos(x-x^2)·(1-2x)}=\frac 00\\&\\&\text{en el denominador aplicamos la fórmula del seno}\\&\text{del ángulo doble}\\&\\&L = \lim_{x\to 0} \frac{e^x - e^{-x}-2x}{(1-2x)sen(2x-2x^2)}\\&\\&\text{derivamos de nuevo}\\&\\&L= \lim_{x\to 0} \frac{e^x+e^{-x}-2}{-2sen(2x-2x^2)+(1-2x)\cos(2x-2x^2)·(2-4x)}=\\&\\&\frac{1+1-2}{-2·0+1·1·2}=\frac{0}{2}=0\end{align}$$Este último era algo enrevesado, vamos a asegurarnos haciendo la gráfica.
Está bien.
Y eso es todo, esos son los límites.
Sa lu dos.
:
:
