Como resuelvo este problema de MCD?

·

·

¡Hola Miguel!

Hay que usar el algoritmo extendido de Euclides, haciendo en cada momento la división entera del número mayor entre el menor y pasando a la siguiente fase el menor y el resto. Cuando se llega a divisor 0 entonces el dividendo es el MCD.

Esos dos últimos datos se pasan en la misma fila a las columnas m, n e iremos completándolas hacia arriba. La nueva columna m será siempre la antigua n. Y la nueva columna n se calcula como la m de la fila de abajo menos el cociente de esa fila por la n de la fila de abajo, es lo que he llamado

n = m'-qn'

Donde con ' quiero referirme a la fila de abajo.

Y cuando se completa la primera fila, los valores de m y n son las constantes tales que

mA + nB = MCD(A,B)

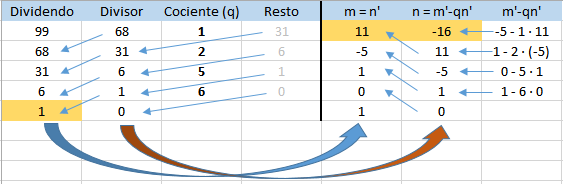
Luego en este caso el MCD es 1 y la combinación lineal es:

11·99 - 16·68 = 1

Si no te gusta ese algoritmo puedes usar el que yo he usado siempre

99 = 68 +31

68 = 2·31 +6

31 = 5·6 + 1

6 = 6·1 + 0

Y el mcd es 1

Y ahora hay que volver hacia atrás desde la penúltima línea

Despejo 1

1 = 31 - 5·6

despejo el 6 en la de arriba

6 = 68 - 2·31

y lo sustituyo

1 = 31 - 5(68 - 2·31)

lo compacto

1 = -5·68 + 11·31

despejo 31 en la fila anterior

31 = 99 - 68

Y lo sustituyo

1 = -5·68 + 11(99-68)

y lo compacto

1 = 11·99 - 16·68

Y ya está, esa es la combinación lineal.

Sa lu dos.

_

_

:)

Jajajaja... ¡No hay problema, Miguel!

:)

.