Vector gradiente perpendicular a la curva de nivel en un punto

·

·

¡Hola Maar!

El vector gradiente siempre es perpendicular a la curva de nivel.

Veamos cuál es el vector gradiente

$$\begin{align}&\nabla z=\left(\frac{\partial z}{\partial x} , \frac{\partial z}{\partial y} \right)=\\&\\&\left(-\frac{2(x-3)-2x}{(x-3)^2}, 1  \right)=\left(\frac{6}{(x-3)^2},1  \right)\\&\\&\text{En el punto (2,-4) será}\\&\\&\nabla z(2,-4)=(6,1)\\&\\&\text{Las líneas de nivel son}\\&\\&c=y - \frac{2x}{x-3}\\&\\&y=f(x) = c + \frac{2x}{x-3}\\&\\&\text{La tangente en (2,-4) será}\\&\\&y = -4 +f'(2)(x-2)\\&\\&f'(x) \text { es la misma que se calculó antes salvo el signo}\\&\\&f'(x)= \frac{-6}{(x-3)^2}\\&\\&f'(2)=-6\\&\\&y= -4-6(x-2)\\&\\&y= -6x+8\\&\\&\text{Dada la pendiente m el vector es } (1,m)\\&\\&\text{El vector tangente a la línea de nivel es }(1,-6)\\&\\&\text{Y el producto escalar del vector gradiente por}\\&\text{el vector tengente a la línea de nivel es}\\&(6,1)·(1-6) = 6-6=0\\&\\&\text{luego son perpendiculares}\\&\end{align}$$

Y esta es la gráfica.  En graficas en tres dimensiones no se puede pedir maravillas, esto es lo mejor que tengo.

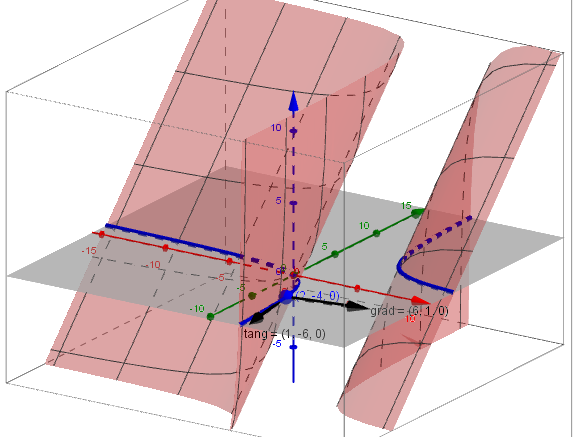
En azul esta la curva de nivel que pasa por (2,-4,0) es decír está en el plano z=0. Está marcado también el azul el punto y tenemos en negro los vectores

Tang=(1,-6,0) que pienso se ve bastante bien que es tangente a la curva de nivel.

Grad=(6,1,0) que si te fijas también se nota que es la dirección hacia la que más crece la función.

Y ambos vectores son perpendiculares, eso hay que hacer el producto escalar para poder asegurarlo, o hacer una imagen en 2D en vez de 3D.

Y eso es todo, saludos.

:

: