Anónimo
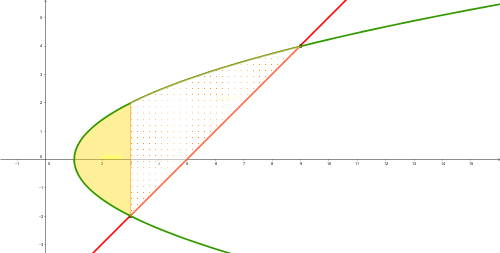
Calcular el área de la región
Me podrian ayudar con este punto calculo de areas :
Calcular el área de la región limitada por
$$\begin{align}&y=x-5\end{align}$$y la recta
$$\begin{align}&y=x-5\end{align}$$
2 Respuestas
;)
Envíame la función correcta
;)
;)
Perdon me confundia la hora de transcribir
Calcular el área de la región limitada por
y^2=2x-2
y la recta
y=x−5
;)
Hola Anónimo Diego!
La región pedida es:
Hallamos los puntos de corte (resolviendo el sistema) y calculamos el área de los dos recintos:
$$\begin{align}&y^2=2x-2\\&y=x-5\\&\\&igualación\\&2x-2=(x-5)^2\\&2x-2=x^2-10x+25\\&\\&x^2-12x+27=0\\&\\&x= \frac{12 \pm \sqrt {12^2-4·27}}{2}= \frac{12 \pm \sqrt {36}}{2}=\\&\\&x_1=9\\&x_2=3\\&\\&R_1=2 \int_1^3 (2x-2)^{\frac{1}{2}}dx=2 \frac{(2x-2)^{\frac{3}{2}}}{\frac{3}{2}}· \frac{1}{ 2}\Bigg ]_1^3=\\&\\&\frac{2}{3} (2x-2)^{\frac{3}{2}} \Bigg|_1^3=\frac{2}{3} \Big(4^{\frac{3}{2}}-0 \Big)=\frac{16}{3} \ \ u^2\\&\\&R_2=\int_3^9 (2x-2)^{\frac{1}{2}}-(x-5)dx=\\&\\&\frac{(2x-2)^\frac{3}{2}}{3}- \frac{x^2}{2}+5x \Bigg|_3^9=\\&\\&\frac{1}{3}16^\frac{3}{2}-\frac{81}{2}+45- \Big(\frac{1}{3}4^\frac{3}{2}-\frac{9}{2}+15 \Big)=\\&\\&=\frac{64}{3}- \frac{81}{2}+45-\frac{8}{3}+\frac{9}{2}-15= \frac{38}{3}\\&\\&A_t=A_1+A_2=\frac{16}{3}+\frac{38}{3}=18 \ \ u^2\end{align}$$saludos
;)
;)
hola lucas muchas gracias por la respuesta ,en qué ecuaciones se reemplaza los valores de 3 a 9 para graficar , ya que la recta me da tal cual como tienes en la gráfica, pero no se como graficar la parábola ¿ en qué ecuación se debe evaluar o que debo hacer ?
;)
Esta parábola, corresponde a dos funciones:
$$\begin{align}&y^2=2x-2\\&\\&y= \pm \sqrt {2x-2}\\&\\&\end{align}$$que corresponden a dos ramas simétricas respecto al eje OX
observa también que :
$$\begin{align}&y^2 \geq0\\&está \ al \ cuadrado\\&lo \ cual \ implica \ que\\&y^2=2x-2\geq0 \Rightarrow x \geq1\end{align}$$Solo tienes que hacer una tabla de valores para esos valores de x>=1, y tomar tanto la raiz positiva como negativa.
x=1 y=0
$$\begin{align}&x=2 \Rightarrow y=\pm \sqrt{4-2}=\pm \sqrt 2\\&(2,\sqrt 2)\\&(2,- \sqrt 2)\\&\\&x=3 \Rightarrow y= \pm \sqrt {2(3)-2}= \pm 2\\&(3,2)\\&(3,-2)\\&x=4 \rightarrow y= \pm \sqrt {2(4)-2}= \pm \sqrt 6\\&(4,+ \sqrt 6)\\&(4,-\sqrt 6)\\&x=9 \rightarrow y= \pm \sqrt {2(9)-2}= \pm 4\\&(9,4)\\&(9,-4)\end{align}$$puedes buscar valores que den soluciones enteras.
Saludos
;)
;)